题目内容
5.设f(x)=lnx,0<x1<x2,若$a=f(\sqrt{{x_1}{x_2}})$,$b=\frac{1}{2}(f({x_1})+f({x_2}))$,$c=f(\frac{{{x_1}+{x_2}}}{2})$,则下列关系式中正确的是( )| A. | a=b<c | B. | a=b>c | C. | b=c<a | D. | b=c>a |
分析 利用对数的运算性质分别化简a,b,c,再利用不等式的性质、对数函数的单调性即可判断出大小关系.
解答 解:∵f(x)=lnx,0<x1<x2,
∴函数f(x)在(0,+∞)上单调递增.
$a=f(\sqrt{{x_1}{x_2}})$=$ln\sqrt{{x}_{1}{x}_{2}}$,$b=\frac{1}{2}(f({x_1})+f({x_2}))$=$\frac{1}{2}(ln{x}_{1}+ln{x}_{2})$=$ln\sqrt{{x}_{1}{x}_{2}}$,$c=f(\frac{{{x_1}+{x_2}}}{2})$=$ln\frac{{x}_{1}+{x}_{2}}{2}$>$ln\sqrt{{x}_{1}{x}_{2}}$,
∴a=b<c.
故选:A.
点评 本题考查了不等式的性质、对数函数的单调性及其运算法则,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
15.如果过点M(-2,0)的直线l与椭圆$\frac{x^2}{2}+{y^2}=1$有公共点,那么直线l的斜率k的取值范围是( )
| A. | $(-∞,-\frac{{\sqrt{2}}}{2}]$ | B. | $[\frac{{\sqrt{2}}}{2},+∞)$ | C. | $[-\frac{1}{2},\frac{1}{2}]$ | D. | $[-\frac{{\sqrt{2}}}{2},\frac{{\sqrt{2}}}{2}]$ |
13.过点(0,-2)的直线l与圆x2+y2=1有公共点,则直线l的倾斜角的取值范围是( )
| A. | $[{\frac{π}{3},\frac{2π}{3}}]$ | B. | $[{\frac{π}{6},\frac{5π}{6}}]$ | C. | $({0,\frac{π}{3}}]∪[{\frac{2π}{3},π})$ | D. | $[{\frac{π}{3},\frac{π}{2}})∪({\frac{π}{2},\frac{2π}{3}}]$ |
15.己知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点为F,右顶点和上顶点分别为A、B,过点F作x轴的垂线与椭圆在第一象限于点P,直线OP交AB于点Q,若|OQ|=|AQ|,则椭圆的离心率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{5}-1}{2}$ |
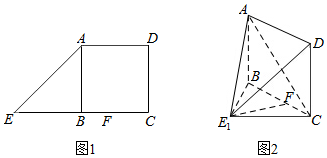 如图1,在直角梯形ADCE中,AD∥EC,EC=2BC,∠ADC=90°,AB⊥EC,点F为线段BC上的一点.将△ABE沿AB折到△ABE1的位置,使E1F⊥BC,如图2.
如图1,在直角梯形ADCE中,AD∥EC,EC=2BC,∠ADC=90°,AB⊥EC,点F为线段BC上的一点.将△ABE沿AB折到△ABE1的位置,使E1F⊥BC,如图2.