Question

10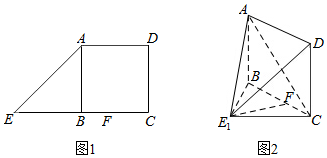．如图1，在直角梯形ADCE中，AD∥EC，EC=2BC，∠ADC=90°，AB⊥EC，点F为线段BC上的一点．将△ABE沿AB折到△ABE₁的位置，使E₁F⊥BC，如图2．
（Ⅰ）求证：AB∥平面CDE₁；
（Ⅱ）求证：E₁F⊥AC；
（Ⅲ）在E₁D上是否存在一点M，使E₁C⊥平面ABM．说明理由．

Answer 1

分析 （Ⅰ）由已知可证AB∥CD，又CD⊆平面CDE₁，AB?平面CDE₁，即可判定AB∥平面CDE₁；
（Ⅱ）由AB⊥BF，AB⊥BE₁，可证AB⊥FE₁，又E₁F⊥BC，可得E₁F⊥平面ABC，从而可证E₁F⊥AC；
（Ⅲ）取CE₁的中点G，连接BG，经点G，在△E₁ CD中作GM∥CD，交E₁ D与点M，连接AM，BM，由CB=BE₁，利用等腰三角形的性质可得CE₁⊥BG，又由CE₁⊥AB，可证CE₁⊥平面ABG，利用GM∥CD∥AB，可知点M在平面ABG上，从而可得E₁C⊥平面ABM．

解答 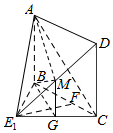证明：（Ⅰ）∵在直角梯形ADCE中，AD∥EC，∠ADC=90°，AB⊥EC，
∴AB∥CD，
∵CD⊆平面CDE₁，AB?平面CDE₁，
∴AB∥平面CDE₁；
（Ⅱ）∵AB⊥BF，AB⊥BE₁，BF∩BE₁=B，
∴AB⊥平面BFE₁，
∵FE₁?平面BFE₁，
∴AB⊥FE₁，
又∵E₁F⊥BC，BC∩AB=B，
∴E₁F⊥平面ABC，
∵AC?平面ABC，
∴E₁F⊥AC；
（Ⅲ）取CE₁的中点G，连接BG，经点G，在△E₁ CD中作GM∥CD，交E₁ D与点M，连接AM，BM，
∵CB=BE₁，
∴CE₁⊥BG，
又∵CE₁⊥AB，AB∩BG=B，
∴CE₁⊥平面ABG，
∵GM∥CD∥AB，
∴点M在平面ABG上，
∴E₁C⊥平面ABM．

点评 本题主要考查了平面与平面垂直的判定，直线与平面平行的判定，直线与平面垂直的判定，考查了空间想象能力和推理论证能力，熟练掌握空间直线与平面之间平行及垂直的判定定理、性质定理、定义、几何特征是解答此类问题的关键，属于中档题．