题目内容
15.己知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点为F,右顶点和上顶点分别为A、B,过点F作x轴的垂线与椭圆在第一象限于点P,直线OP交AB于点Q,若|OQ|=|AQ|,则椭圆的离心率为( )| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{5}-1}{2}$ |
分析 由已知得∠POF=∠BAO,∠PFO=∠BOA,从而△POF∽△BOA,由此能求出椭圆的离心率.
解答  解:∵椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点为F,右顶点和上顶点分别为A、B,
解:∵椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点为F,右顶点和上顶点分别为A、B,
过点F作x轴的垂线与椭圆在第一象限于点P,直线OP交AB于点Q,|OQ|=|AQ|,
∴∠POF=∠BAO,∠PFO=∠BOA,∴△POF∽△BOA,
∴$\frac{OF}{OA}$=$\frac{PF}{OB}$,即$\frac{c}{a}$=$\frac{\frac{{b}^{2}}{a}}{b}$,∴$\frac{c}{a}=\frac{b}{a}$,∴b=c,a=$\sqrt{2}c$
∴椭圆的离心率为:e=$\frac{c}{a}$=$\frac{c}{\sqrt{2}c}=\frac{\sqrt{2}}{2}$.
故选:B.
点评 本题考查椭圆的离心率的求法,是中档题,解题时要认真审题,注意椭圆性质和数形结合思想的合理运用.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案
相关题目
5.设f(x)=lnx,0<x1<x2,若$a=f(\sqrt{{x_1}{x_2}})$,$b=\frac{1}{2}(f({x_1})+f({x_2}))$,$c=f(\frac{{{x_1}+{x_2}}}{2})$,则下列关系式中正确的是( )
| A. | a=b<c | B. | a=b>c | C. | b=c<a | D. | b=c>a |
6.若圆锥的侧面展开图的圆心角为90°,半径为r,则该圆锥的全面积为( )
| A. | $\frac{π{r}^{2}}{16}$ | B. | $\frac{3π{r}^{2}}{16}$ | C. | $\frac{π{r}^{2}}{4}$ | D. | $\frac{5π{r}^{2}}{16}$ |
10.曲线f(x)=$\frac{-4}{\sqrt{3}({e}^{x}+1)}$在点(0,f(0))处的切线方程为( )
| A. | x-$\sqrt{3}$y-2=0 | B. | $\sqrt{3}$x+y-2=0 | C. | x-$\sqrt{3}$y+2=0 | D. | $\sqrt{3}$x+y+2=0 |
4.已知某几何体的三视图如图所示,则该几何体的表面积为( )
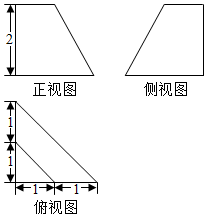

| A. | $\frac{7}{3}$ | B. | $\frac{17}{2}$ | C. | 13 | D. | $\frac{17+3\sqrt{10}}{2}$ |
5.函数y=$\root{3}{{x}^{2}}$-x2+2的图象在以点(1,y1)为切点的切线与坐标轴所围成的三角形面积等于( ),函数y=x3图象上过点(1,y2)的切线与两条坐标轴所围成的三角形面积等于( )
| A. | $\frac{25}{6}$ | B. | $\frac{2}{3}$ | C. | $\frac{2}{3}$或$\frac{1}{24}$ | D. | $\frac{15}{4}$ | ||||
| E. | $\frac{7}{3}$ | F. | $\frac{15}{4}$或$\frac{7}{3}$ |