题目内容
16.已知直线l的一个方向向量的坐标是$({-1,\sqrt{3}})$,则直线l的倾斜角为$\frac{2π}{3}$.分析 设直线l的倾斜角为θ,θ∈[0,π),则tanθ=-$\sqrt{3}$,即可得出.
解答 解:设直线l的倾斜角为θ,θ∈[0,π),则tanθ=-$\sqrt{3}$,
∴θ=$\frac{2π}{3}$.
故答案为:$\frac{2π}{3}$.
点评 本题考查了直线方向向量、倾斜角与斜率的关系,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
4.设向量$\overrightarrow{a}$,$\overrightarrow{b}$满足|$\overrightarrow{a}$|=|$\overrightarrow{b}$|=1,$\overrightarrow{a}$•$\overrightarrow{b}$=$\frac{1}{2}$,则|$\overrightarrow{a}$+$\overrightarrow{b}$|等于( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\sqrt{5}$ | D. | $\sqrt{7}$ |
5.设f(x)=lnx,0<x1<x2,若$a=f(\sqrt{{x_1}{x_2}})$,$b=\frac{1}{2}(f({x_1})+f({x_2}))$,$c=f(\frac{{{x_1}+{x_2}}}{2})$,则下列关系式中正确的是( )
| A. | a=b<c | B. | a=b>c | C. | b=c<a | D. | b=c>a |
6.若圆锥的侧面展开图的圆心角为90°,半径为r,则该圆锥的全面积为( )
| A. | $\frac{π{r}^{2}}{16}$ | B. | $\frac{3π{r}^{2}}{16}$ | C. | $\frac{π{r}^{2}}{4}$ | D. | $\frac{5π{r}^{2}}{16}$ |
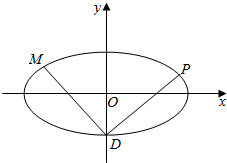 椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0).
椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0).