题目内容
15.如果过点M(-2,0)的直线l与椭圆$\frac{x^2}{2}+{y^2}=1$有公共点,那么直线l的斜率k的取值范围是( )| A. | $(-∞,-\frac{{\sqrt{2}}}{2}]$ | B. | $[\frac{{\sqrt{2}}}{2},+∞)$ | C. | $[-\frac{1}{2},\frac{1}{2}]$ | D. | $[-\frac{{\sqrt{2}}}{2},\frac{{\sqrt{2}}}{2}]$ |
分析 设过点M(-2,0)的直线l的方程为y=k(x+2),与椭圆方程联立,得(2k2+1)x2+8k2x+8k2-2=0,由此利用根的判别式能求出直线l的斜率k的取值范围.
解答 解:设过点M(-2,0)的直线l的方程为y=k(x+2),
联立$\left\{\begin{array}{l}{y=k(x+2)}\\{\frac{{x}^{2}}{2}+{y}^{2}=1}\end{array}\right.$,得(2k2+1)x2+8k2x+8k2-2=0,
∵过点M(-2,0)的直线l与椭圆$\frac{x^2}{2}+{y^2}=1$有公共点,
∴△=64k4-4(2k2+1)(8k2-2)≥0,
整理,得k2$≤\frac{1}{2}$,
解得-$\frac{\sqrt{2}}{2}$≤k≤$\frac{\sqrt{2}}{2}$.
∴直线l的斜率k的取值范围是[-$\frac{\sqrt{2}}{2}$,$\frac{\sqrt{2}}{2}$].
故选:D.
点评 本题考查直线的斜率的取值范围的求法,是基础题,解题时要认真审题,注意根的判别式的合理运用.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
3.已知集合A={1,2,3,4,5},集合B={-2,2,3,4,5,9},则集合A∩B=( )
| A. | {2,3,4} | B. | {2,3,4,5} | C. | {1,2,3,4,5} | D. | {-2,1,2,3,4,5} |
10.有3个活动小组,甲、乙两位同学各自参加其中一个小组,每位同学参加各个小组的可能性相同,则这两位同学不在一个兴趣小组的概率为( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
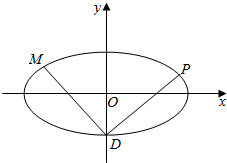 椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0).
椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0).