题目内容
13.在正四面体ABCD中,E是BC边的中点,则AE与BD所成角的余弦值为$\frac{\sqrt{3}}{6}$.分析 作AO⊥平面BCD,交平面BCD于点O,取BD中点F,以O为原点,OF为x轴,OE为y轴,OA为z轴,建立空间直角坐标系,利用向量法能求出AE与BD所成角的余弦值.
解答  解:作AO⊥平面BCD,交平面BCD于点O,取BD中点F,
解:作AO⊥平面BCD,交平面BCD于点O,取BD中点F,
以O为原点,OF为x轴,OE为y轴,OA为z轴,建立空间直角坐标系,
设正四面体ABCD的棱长为2,则A(0,0,$\frac{2\sqrt{6}}{3}$),
E(0,$\frac{\sqrt{3}}{3}$,0),B(1,$\frac{\sqrt{3}}{3}$,0),D(0,-$\frac{2\sqrt{3}}{3}$,0),
$\overrightarrow{AE}$=(0,$\frac{\sqrt{3}}{3}$,-$\frac{2\sqrt{6}}{3}$),$\overrightarrow{BD}$=(-1,$\sqrt{3}$,0),
设AE与BD所成角为θ,
则cosθ=$\frac{|\overrightarrow{AE}•\overrightarrow{BD}|}{|\overrightarrow{AE}|•|\overrightarrow{BD}|}$=$\frac{1}{\sqrt{3}×2}$=$\frac{{\sqrt{3}}}{6}$.
∴AE与BD所成角的余弦值为$\frac{\sqrt{3}}{6}$.
故答案为:$\frac{\sqrt{3}}{6}$.
点评 本题考查异面直线的求法,是中档题,解题时要认真审题,注意向量法的合理运用.

练习册系列答案
相关题目
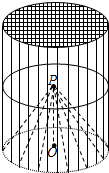 某种“笼具”由内,外两层组成,无下底面,内层和外层分别是一个圆锥和圆柱,其中圆柱与圆锥的底面周长相等,圆柱有上底面,制作时需要将圆锥的顶端剪去,剪去部分和接头忽略不计,已知圆柱的底面周长为24πcm,高为30cm,圆锥的母线长为20cm.
某种“笼具”由内,外两层组成,无下底面,内层和外层分别是一个圆锥和圆柱,其中圆柱与圆锥的底面周长相等,圆柱有上底面,制作时需要将圆锥的顶端剪去,剪去部分和接头忽略不计,已知圆柱的底面周长为24πcm,高为30cm,圆锥的母线长为20cm.