题目内容
17．函数f（x）=$\frac{1}{{4}^{x}+1}$图象的对称中心为（0，$\frac{1}{2}$）．分析 由f（x）=$\frac{1}{{4}^{x}+1}$可得f（x）+f（-x）=$\frac{1}{{4}^{x}+1}$+$\frac{{4}^{x}}{{4}^{x}+1}$=1，从而可得函数f（x）的图象的对称中心为（0，$\frac{1}{2}$）．
解答 解：∵f（x）=$\frac{1}{{4}^{x}+1}$，
∴f（-x）=$\frac{1}{{4}^{-x}+1}$=$\frac{{4}^{x}}{{4}^{x}+1}$，
∴f（x）+f（-x）=$\frac{1}{{4}^{x}+1}$+$\frac{{4}^{x}}{{4}^{x}+1}$=1，
∴函数f（x）=$\frac{1}{{4}^{x}+1}$图象的对称中心为（0，$\frac{1}{2}$），
故答案为：（0，$\frac{1}{2}$）．
点评 本题考查了函数的化简与运算的应用及数形结合的思想应用．
练习册系列答案
名校通行证有效作业系列答案
相关题目
12．在掷均匀硬币的试验中，以下对“大数定理”的理解错误的是（ ）
| A． | 大量的试验中，出现正面的频率稳定于$\frac{1}{2}$ | |
| B． | 不管试验多少次，出现正面的概率始终为$\frac{1}{2}$ | |
| C． | 试验次数增多，出现正面的经验概率越接近$\frac{1}{2}$ | |
| D． | 试验次数无限增大时，出现正面的频率的极限为$\frac{1}{2}$ |
9．
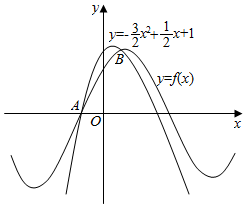如图所示，函数f（x）=sin（ωx+φ）（ω＞0，|φ|＜$\frac{π}{2}$）的图象与二次函数y=-$\frac{3}{2}$x2+$\frac{1}{2}$x+1的图象交于A（x1，0）和B（x2，1），则f（x）的解析式为（ ）
如图所示，函数f（x）=sin（ωx+φ）（ω＞0，|φ|＜$\frac{π}{2}$）的图象与二次函数y=-$\frac{3}{2}$x2+$\frac{1}{2}$x+1的图象交于A（x1，0）和B（x2，1），则f（x）的解析式为（ ）| A． | f（x）=sin（$\frac{1}{6}$x+$\frac{π}{3}$） | B． | f（x）=sin（$\frac{1}{2}$x+$\frac{π}{3}$） | C． | f（x）=sin（$\frac{π}{2}$x+$\frac{π}{3}$） | D． | f（x）=sin（$\frac{π}{2}$x+$\frac{π}{6}$） |