题目内容
5．圆x2+y2-2x-2y+1=0上的点到直线x-y=2的距离的最大值是$\sqrt{2}$+1．分析 把圆的方程化为标准方程后，找出圆心坐标和半径r，利用点到直线的距离公式求出圆心到已知直线的距离d，求出d+r即为所求的距离最大值．
解答 解：把圆的方程化为标准方程得：（x-1）2+（y-1）2=1，
所以圆心坐标为（1，1），圆的半径r=1，
所以圆心到直线x-y=2的距离d=$\frac{|1-1-2|}{\sqrt{2}}$=$\sqrt{2}$，
则圆上的点到直线x-y=2的距离最大值为d+r=$\sqrt{2}$+1．
故答案为：$\sqrt{2}$+1
点评 本题主要考查直线与圆的位置关系，当考查圆上的点到直线的距离问题，基本思路是：先求出圆心到直线的距离，最大值时，再加上半径，最小值时，再减去半径．
练习册系列答案
期末1卷素质教育评估卷系列答案
相关题目
9．
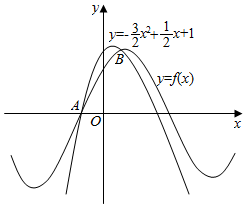如图所示，函数f（x）=sin（ωx+φ）（ω＞0，|φ|＜$\frac{π}{2}$）的图象与二次函数y=-$\frac{3}{2}$x2+$\frac{1}{2}$x+1的图象交于A（x1，0）和B（x2，1），则f（x）的解析式为（ ）
如图所示，函数f（x）=sin（ωx+φ）（ω＞0，|φ|＜$\frac{π}{2}$）的图象与二次函数y=-$\frac{3}{2}$x2+$\frac{1}{2}$x+1的图象交于A（x1，0）和B（x2，1），则f（x）的解析式为（ ）| A． | f（x）=sin（$\frac{1}{6}$x+$\frac{π}{3}$） | B． | f（x）=sin（$\frac{1}{2}$x+$\frac{π}{3}$） | C． | f（x）=sin（$\frac{π}{2}$x+$\frac{π}{3}$） | D． | f（x）=sin（$\frac{π}{2}$x+$\frac{π}{6}$） |
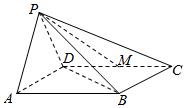如图所示，在四棱锥P-ABCD中，底面ABCD为菱形，且∠DAB=60°，PA=PD，M为CD的中点，BD⊥PM．
15．设集合M={x|x2-x-6＜0}，N={x|x-1＞0}，则M∩N=（ ）
| A． | （1，2） | B． | （1，3） | C． | （-1，2） | D． | （-1，3） |