题目内容
1.Sn是数列{an}的前n项和,已知an>0,$\frac{{{a_n}+1}}{2}=\sqrt{S_n}$.(Ⅰ)求{an}的通项公式;
(Ⅱ)求数列$\left\{{\frac{a_n}{2^n}}\right\}$的前n项和.
分析 (Ⅰ)$\frac{{{a_n}+1}}{2}=\sqrt{S_n}$化为$a_n^2+2{a_n}+1=4{S_n}$,再利用递推关系、等差数列的通项公式即可得出;
(Ⅱ)设$\left\{{\frac{a_n}{2^n}}\right\}$前n项和为Tn,由(Ⅰ)知$\frac{a_n}{2^n}=\frac{2n-1}{2^n}$,再利用“错位相减法”、等比数列的前n项和公式即可得出.
解答 解:(Ⅰ)$\frac{{{a_n}+1}}{2}=\sqrt{S_n}$化为$a_n^2+2{a_n}+1=4{S_n}$,可知$a_{n+1}^2+2{a_{n+1}}+1=4{S_{n+1}}$,
可得$a_{n+1}^2-{a_n}^2+2({a_{n+1}}-{a_n})=4{a_{n+1}}$,即(an+1+an)(an+1-an)=2(an+1+an),
由于an>0,可得an+1-an=2,
又$a_1^2+2{a_1}+1=4{a_1}$,解得a1=1,
∴{an}是首项是1,公差是2的等差数列,通项公式是an=2n-1.
(Ⅱ)设$\left\{{\frac{a_n}{2^n}}\right\}$前n项和为Tn,由(Ⅰ)知$\frac{a_n}{2^n}=\frac{2n-1}{2^n}$,
则${T_n}=\frac{1}{2}+\frac{3}{2^2}+\frac{5}{2^3}+…+\frac{2n-1}{2^n}$,$\frac{1}{2}{T_n}=\frac{1}{2^2}+\frac{3}{2^3}+\frac{5}{2^4}+…+\frac{2n-1}{{{2^{n+1}}}}$,
两式相减得$\frac{1}{2}{T_n}=\frac{1}{2}+\frac{2}{2^2}+\frac{2}{2^3}+\frac{2}{2^4}+…+\frac{2}{2^n}-\frac{2n-1}{{{2^{n+1}}}}$,
即$\frac{1}{2}{T_n}=\frac{1}{2}+\frac{{\frac{2}{2^2}-\frac{2}{2^n}•\frac{1}{2}}}{{1-\frac{1}{2}}}-\frac{2n-1}{{{2^{n+1}}}}$,
所以${T_n}=3-\frac{2n+3}{2^n}$.
点评 本题考查了“错位相减法”、等差数列与等比数列的通项公式及其前n项和公式、递推关系,考查了推理能力与计算能力,属于中档题.

 名校课堂系列答案
名校课堂系列答案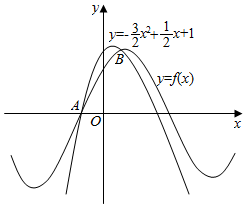 如图所示,函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的图象与二次函数y=-$\frac{3}{2}$x2+$\frac{1}{2}$x+1的图象交于A(x1,0)和B(x2,1),则f(x)的解析式为( )
如图所示,函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的图象与二次函数y=-$\frac{3}{2}$x2+$\frac{1}{2}$x+1的图象交于A(x1,0)和B(x2,1),则f(x)的解析式为( )| A. | f(x)=sin($\frac{1}{6}$x+$\frac{π}{3}$) | B. | f(x)=sin($\frac{1}{2}$x+$\frac{π}{3}$) | C. | f(x)=sin($\frac{π}{2}$x+$\frac{π}{3}$) | D. | f(x)=sin($\frac{π}{2}$x+$\frac{π}{6}$) |
| A. | 若a2≥b,则a≥$\sqrt{b}$或a≤-$\sqrt{b}$ | B. | 若a2≥b,则a>$\sqrt{b}$或a<-$\sqrt{b}$ | ||
| C. | 若a≥$\sqrt{b}$或a≤-$\sqrt{b}$,则a2≥b | D. | 若a>$\sqrt{b}$或a<-$\sqrt{b}$,则a2≥b |