题目内容
设a＞b＞c＞1，记M=a-
，N=a-
，P=2（
-
），Q=3（
-
），试找出中的最小者，并说明理由．
| c |
| b |
| a+b |
| 2 |
| ab |
| a+b+c |
| 3 |
| 3 | abc |
考点：不等式比较大小
专题：不等式的解法及应用
分析：作差比较法比较N与M的大小，同理由作差法比较和综合法比较P与Q的大小，再比较两者的小者．
解答：
解：∵b＞c＞1，
∴
＞
，
∴-
＜-
∴a-
＞a-
，
∴M＞N，
又Q-P=P=3（
-
）-2（
-
）=c+2
-3
=c+
+
-3
≥3
-3
=0，
又a＞b＞c＞1，
∴c≠
，
从而Q＞P，
又N-P=2
-
-b=
(2
-1-
)=
[(
-1)+(
-
)]＞0，
∴P＜N，
故P最小．
∴
| b |
| c |
∴-
| b |
| c |
∴a-
| c |
| b |
∴M＞N，
又Q-P=P=3（
| a+b+c |
| 3 |
| 3 | abc |
| a+b |
| 2 |
| ab |
| ab |
| 3 | abc |
| ab |
| ab |
| 3 | abc |
| 3 | c•
| ||||
| 3 | abc |
又a＞b＞c＞1，
∴c≠
| ab |
从而Q＞P，
又N-P=2
| ab |
| b |
| b |
| a |
| b |
| b |
| a |
| a |
| b |
∴P＜N，
故P最小．
点评：本题主要考查了不等式的大小比，作差法式常用的方法，属于基础题．
练习册系列答案
相关题目
如图，已知AB是圆柱OO1底面圆O的直径，底面半径R=1，圆柱的表面积为8π；点C在底面圆O上，且直线A1C与下底面所成的角的大小为60°．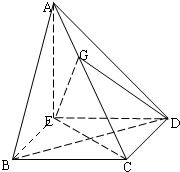
如图，在四棱锥A-BCDE中，AE⊥平面BCDE，∠ABC=∠BCD=∠CDA=90°，AC=6