题目内容
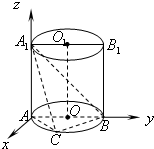
 如图,已知AB是圆柱OO1底面圆O的直径,底面半径R=1,圆柱的表面积为8π;点C在底面圆O上,且直线A1C与下底面所成的角的大小为60°.
如图,已知AB是圆柱OO1底面圆O的直径,底面半径R=1,圆柱的表面积为8π;点C在底面圆O上,且直线A1C与下底面所成的角的大小为60°.(1)求点A到平面A1CB的距离;
(2)求二面角A-A1B-C的大小(结果用反三角函数值表示).
考点:二面角的平面角及求法,点、线、面间的距离计算
专题:综合题,空间位置关系与距离,空间角
分析:(1)确定∠A1CA是直线A1C与下底面所成的角,以A为坐标原点,以AB、AA1分别为y、z轴建立空间直角坐标系,求出平面A1CB的一个法向量,利用距离公式,即可求点A到平面A1CB的距离;
(2)平面A1AB的一个法向量为
=(1,0,0),由(1)知平面A1CB的一个法向量
=(
,
,1),利用向量的夹角公式,即可求二面角A-A1B-C的大小.
(2)平面A1AB的一个法向量为
| m |
| n |
| ||
| 2 |
| 3 |
| 2 |
解答:
 解:(1)设AA1=h,因为底面半径R=1,圆柱的表面积为8π,
解:(1)设AA1=h,因为底面半径R=1,圆柱的表面积为8π,
所以2π×12+2πh=8π,解得h=3.
因为AA1⊥底面ACB,所以AC是A1C在底面ACB上的射影,
所以∠A1CA是直线A1C与下底面所成的角,即∠A1CA=60°
在直角三角形A1CA中,A1A=3,∠A1CA=60°,所以AC=
.
AB是底面直径,所以∠CAB=
.
以A为坐标原点,以AB、AA1分别为y、z轴建立空间直角坐标系如图所示:
则A(0,0,0)、C(
,
,0)、A1(0,0,3)、B(0,2,0),
于是
=(
,
,0),
=(0,2,3),
=(-
,
,0)
设平面A1CB的一个法向量为
=(x,y,z),则
,
不妨令z=1,则
=(
,
,1),
所以A到平面A1CB的距离d=
=
所以点A到平面A1CB的距离为
.
(2)平面A1AB的一个法向量为
=(1,0,0)
由(1)知平面A1CB的一个法向量
=(
,
,1),
二面角A-A1B-C的大小为θ,则|cosθ|=
.
由于二面角A-A1B-C为锐角,所以二面角A-A1B-C的大小为arccos
.
 解:(1)设AA1=h,因为底面半径R=1,圆柱的表面积为8π,
解:(1)设AA1=h,因为底面半径R=1,圆柱的表面积为8π,所以2π×12+2πh=8π,解得h=3.
因为AA1⊥底面ACB,所以AC是A1C在底面ACB上的射影,
所以∠A1CA是直线A1C与下底面所成的角,即∠A1CA=60°
在直角三角形A1CA中,A1A=3,∠A1CA=60°,所以AC=
| 3 |
AB是底面直径,所以∠CAB=
| π |
| 6 |
以A为坐标原点,以AB、AA1分别为y、z轴建立空间直角坐标系如图所示:
则A(0,0,0)、C(
| ||
| 2 |
| 3 |
| 2 |
于是
| AC |
| ||
| 2 |
| 3 |
| 2 |
| A1B |
| CB |
| ||
| 2 |
| 1 |
| 2 |
设平面A1CB的一个法向量为
| n |
|
不妨令z=1,则
| n |
| ||
| 2 |
| 3 |
| 2 |
所以A到平面A1CB的距离d=
|
| ||||
|
|
| 3 |
| 2 |
所以点A到平面A1CB的距离为
| 3 |
| 2 |
(2)平面A1AB的一个法向量为
| m |
由(1)知平面A1CB的一个法向量
| n |
| ||
| 2 |
| 3 |
| 2 |
二面角A-A1B-C的大小为θ,则|cosθ|=
| ||
| 4 |
由于二面角A-A1B-C为锐角,所以二面角A-A1B-C的大小为arccos
| ||
| 4 |
点评:本题考查二面角大小的计算,考查点到平面距离的计算,正确运用向量方法是关键.

练习册系列答案
相关题目
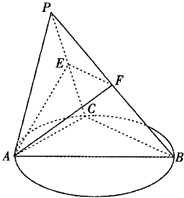 如图,C是以AB为直径的圆O上异于A,B的点,平面PAC⊥平面ABC,PA=PC=AC=2,BC=4,E,F 分别是PC,PB的中点,记平面AEF与平面ABC的交线为直线l.
如图,C是以AB为直径的圆O上异于A,B的点,平面PAC⊥平面ABC,PA=PC=AC=2,BC=4,E,F 分别是PC,PB的中点,记平面AEF与平面ABC的交线为直线l.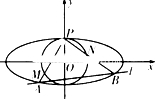 如图,椭圆C:
如图,椭圆C: