题目内容
观察下列问题:
已知(1-2x)2013=a0+a1x+a2x2+a3x3+…+a2013x2013,
令x=1,可得a0+a1+a2+…+a2013=(1-2•1)2013=-1,
令x=1,可得a0-a1+a2+…-a2013=(1+2•1)2013=32013,
请仿照这种“赋值法”,令x=0,得到a0= ,并求出
+
+
+…+
= .
已知(1-2x)2013=a0+a1x+a2x2+a3x3+…+a2013x2013,
令x=1,可得a0+a1+a2+…+a2013=(1-2•1)2013=-1,
令x=1,可得a0-a1+a2+…-a2013=(1+2•1)2013=32013,
请仿照这种“赋值法”,令x=0,得到a0=
| a1 |
| 2 |
| a2 |
| 22 |
| a3 |
| 23 |
| a2013 |
| 22013 |
考点:归纳推理
专题:推理和证明
分析:仿照这种“赋值法”,令x=0,可得a0=1,再令x=0,可得a0=1,从而求得出
+
+
+…+
.
| a1 |
| 2 |
| a2 |
| 22 |
| a3 |
| 23 |
| a2013 |
| 22013 |
解答:
解:∵已知(1-2x)2013=a0+a1x+a2x2+a3x3+…+a2013x2013
令x=0,可得a0=(1-0)2013=0,
再令x=0,可得a0=1,
则
+
+
+…+
=0-1=-1,
故答案为:1,-1
令x=0,可得a0=(1-0)2013=0,
再令x=0,可得a0=1,
则
| a1 |
| 2 |
| a2 |
| 22 |
| a3 |
| 23 |
| a2013 |
| 22013 |
故答案为:1,-1
点评:本题主要考查二项式定理的应用,注意根据题意,分析所给代数式的特点,通过给二项式的x赋值,求展开式的系数和,可以简便的求出答案,属于中档题.

练习册系列答案
相关题目
已知f(x)=
,若函数g(x)=f(x)-kx+k只有一个零点,则k的取值范围是( )
|
| A、(-∞,-1)∪(1,+∞) |
| B、(-1,1) |
| C、[0,1] |
| D、(-∞,-1]∪[0,1] |
已知a>0,设p:存在a∈R,使y=ax是R上的单调递减函数; q:存在a∈R,使函数g(x)=lg(2ax2+2x+1)的值域为R,如果“p∧q”为假,“p∨q”为真,则a的取值范围是( )
A、(
| ||
B、(
| ||
C、(0,
| ||
D、(0,
|
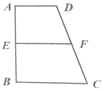 如图梯形ABCD中,AD∥BC,∠ABC=90°,AD:BC:AB=2:3:4,E、F分别是AB,CD的中点,将四边形ADFE沿直线EF进行翻折.给出四个结论:
如图梯形ABCD中,AD∥BC,∠ABC=90°,AD:BC:AB=2:3:4,E、F分别是AB,CD的中点,将四边形ADFE沿直线EF进行翻折.给出四个结论: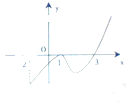 如图是函数y=f(x)的导函数y=f′(x)的图象,给出下列命题:
如图是函数y=f(x)的导函数y=f′(x)的图象,给出下列命题: