题目内容
在正方体ABCD-A1B1C1D1中,E、F分别是正方形A1B1C1D1、ADD1A1的中心,求证:平面DEF∥平面AB1C.
考点:平面与平面平行的判定
专题:空间位置关系与距离,空间向量及应用
分析:以D为原点,分别以DA,DC,DD1所在直线为x,y,z轴建立空间直角坐标系,将D,E,F,A,B1,C得坐标写出,利用向量得坐标关系判断EF∥AB1,DF∥CB1,利用面面平行得判定定理可得.
解答:
解:以D为原点,分别以DA,DC,DD1所在直线为x,y,z轴建立空间直角坐标系,设正方体棱长为2,则D(0,0,0),E(1,1,2),F(1,0,1),A(2,0,0),C(0,2,0),B1(2,2,2),
所以
=(0,-1,-1),
=(1,0,1),
=(0,2,2),
=(2,0,2),
所以
∥
,
∥
,并且EF∩DF=F,AB1∩CB1=B1,
所以平面DEF∥平面AB1C.
所以
| EF |
| DF |
| AB1 |
| CB1 |
所以
| EF |
| AB1 |
| DF |
| CB1 |
所以平面DEF∥平面AB1C.
点评:本题借助于空间向量解决了平面平行得判断,关键是正确建立空间直角坐标系,得到向量平行与平面内的直线平行,从而判断面面平行.

练习册系列答案
相关题目
下列结论错误的是( )
| A、命题:“若a>b>0,则a2>b2”的逆命题是假命题 | ||||||||
| B、若函数f(x)可导,则f′(x0)是x0为函数极值点的必要不充分条件 | ||||||||
C、向量
| ||||||||
| D、命题p:“?x∈R,ex≥x+1”的否定是“?x∈R,ex<x+1” |
 如图,E、F分别是三棱锥P-ABC的棱AP、BC的中点,PC=10,AB=6,EF=7,则异面直线AB与PC所成的角为( )
如图,E、F分别是三棱锥P-ABC的棱AP、BC的中点,PC=10,AB=6,EF=7,则异面直线AB与PC所成的角为( )| A、30° | B、60° |
| C、0° | D、120° |
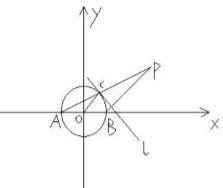 已知A,B是⊙0:x2+y2=4与x轴的两个交点,C是⊙O上异于点A,B的任意一点,过点B作直线l的垂线BP,且与AC的延长线交于点P,求点P的轨迹方程.
已知A,B是⊙0:x2+y2=4与x轴的两个交点,C是⊙O上异于点A,B的任意一点,过点B作直线l的垂线BP,且与AC的延长线交于点P,求点P的轨迹方程.