题目内容
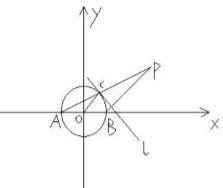已知A，B是⊙0：x2+y2=4与x轴的两个交点，C是⊙O上异于点A，B的任意一点，过点B作直线l的垂线BP，且与AC的延长线交于点P，求点P的轨迹方程．考点：椭圆的定义
专题：圆锥曲线的定义、性质与方程
分析：设P（x，y）．由题意可得C（-1+
，
），由C在圆上，代入即可得出点P的轨迹方程．
| x |
| 2 |
| y |
| 2 |
解答：
解：设P（x，y）．连接OC，则OC⊥过点C的切线l，
∵BP⊥点C的切线，∴OC∥BP
∵OA=OB，∴CA=CP即C是AP的中点．
∵A（-2，0），P（x，y），∴C（-1+
，
），
∵C在圆上
∴（-1+
）2+（
）2=4
即点P的轨迹方程是：x2-4x+y2=12．
∵BP⊥点C的切线，∴OC∥BP
∵OA=OB，∴CA=CP即C是AP的中点．
∵A（-2，0），P（x，y），∴C（-1+
| x |
| 2 |
| y |
| 2 |
∵C在圆上
∴（-1+
| x |
| 2 |
| y |
| 2 |
即点P的轨迹方程是：x2-4x+y2=12．
点评：本题主要考查点的轨迹方程的求法--代入法的运用，属于基础题．
练习册系列答案
A加金题 系列答案
全优测试卷系列答案
相关题目
下列说法错误的是（ ）
| A、命题“若a=0，则ab=0”的否命题是：“若a≠0，则ab≠0” | ||
| B、如果命题“￢p”与命题“p或q”都是真命题，那么命题q一定是真命题 | ||
| C、若命题p：?x∈R，x2-x+1＜0，则￢p：?x∈R，x2-x+1≥0 | ||
D、“sinθ=
|
若点M在直线a上，a在平面α内，则M，a，α间的上述关系的集合表示可记作（ ）
| A、M∈a∈α |
| B、M∈a⊆α |
| C、M⊆a⊆α |
| D、M⊆a∈α |