题目内容
曲线y2=4ax与x=a围成的平面区域绕x轴旋转所得的旋转体的体积为 .
考点:定积分
专题:计算题,导数的概念及应用
分析:根据积分的几何意义得出曲线y2=4ax与x=a围成的平面区域绕x轴旋转所得的旋转体的体积,求解即可V=π×∫
4axdx=π×2ax2|
=2πa3.
a 0 |
a 0 |
解答:
解:∵曲线y2=4ax与x=a围成的平面区域绕x轴旋转所得的旋转体的体积,
∴V=π×∫
4axdx=π×2ax2|
=2πa3,
故答案为:2πa3
∴V=π×∫
a 0 |
a 0 |
故答案为:2πa3
点评:本题考查了曲线的旋转问题,运用积分求解体积,属于计算题.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
若全集U=R,集合A={x|x2+x-2≤0},B={y|y=log2(x+3),x∈A},则集合A∩(∁UB)=( )
| A、{x|-2≤x<0} |
| B、{x|0≤x≤1} |
| C、{x|-3<x≤-2} |
| D、{x|x≤-3} |
在半径为R球面上有A,B,C三点,且AB=8
,∠ACB=60°,球心O到平面ABC的距离为6,则半径R=( )
| 3 |
| A、8 | B、10 | C、12 | D、14 |

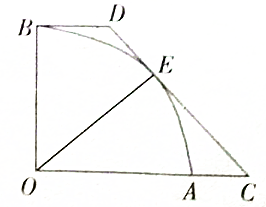 如图,扇形AOB的半径OA=2,∠AOB=
如图,扇形AOB的半径OA=2,∠AOB=