题目内容
设实数x,y满足
,则动点P(x,y)所形成区域的面积为 ,z=|x-2y+2|的取值范围是 .
|
考点:简单线性规划
专题:计算题,作图题,不等式的解法及应用
分析:由题意作出其平面区域,从而利用三角形的面积公式求面积,再由z=|x-2y+2|的几何意义是阴影内的点到直线x-2y+2=0的距离的
倍求其取值范围,从而解得.
| 5 |
解答:
解:由题意作出其平面区域,
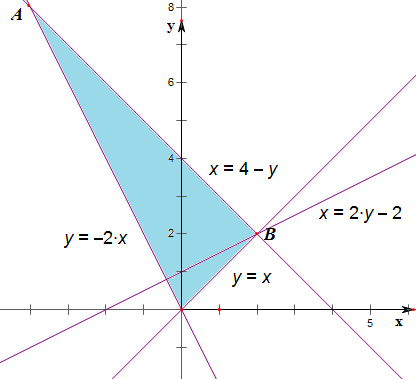
可知A(-4,8),B(2,2);
故动点P(x,y)所形成区域的面积S=
×4×(4+2)=12;
z=|x-2y+2|的几何意义是阴影内的点到直线x-2y+2=0的距离的
倍;
故0≤|x-2y+2|≤|-4-2×8+2|=18;
即0≤z≤18;
故答案为:12,[0,18].

可知A(-4,8),B(2,2);
故动点P(x,y)所形成区域的面积S=
| 1 |
| 2 |
z=|x-2y+2|的几何意义是阴影内的点到直线x-2y+2=0的距离的
| 5 |
故0≤|x-2y+2|≤|-4-2×8+2|=18;
即0≤z≤18;
故答案为:12,[0,18].
点评:本题考查了简单线性规划,作图要细致认真,用到了表达式的几何意义的转化,属于中档题.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
设函数f(x)=x|x-a|,若对?x1,x2∈[3,+∞),x1≠x2,不等式
>0恒成立,则实数a的取值范围是( )
| f(x1)-f(x2) |
| x1-x2 |
| A、(-∞,-3] |
| B、[-3,0) |
| C、(-∞,3] |
| D、(0,3] |
已知定义在R上的函数y=f(x)满足f(x+2)=f(x),当-1<x≤1时,f(x)=x,若函数g(x)=f(x)-loga|x|至少有5个零点,则a的取值范围是( )
| A、(1,5) | ||
B、(0,
| ||
C、(0,
| ||
D、[
|
在△ABC中,已知∠A=30°,AB=
,BC=1,则AC的长为( )
| 3 |
| A、2 | B、1 | C、2或1 | D、4 |
已知定义在R上的奇函数f(x),满足f(x-4)=-f(x)且在区间[0,2]上是增函数,则( )
| A、f(-25)<f(11)<f(80) |
| B、f(80)<f(11)<f(-25) |
| C、f(11)<f(80)<f(-25) |
| D、f(-25)<f(80)<f(11) |