题目内容
已知函数f(x)=cosx•sin(x+
)-
cos2x+
,x∈R则f(x)在闭区间[-
,
]上的最大值和最小值分别为 .
| π |
| 3 |
| 3 |
| ||
| 4 |
| π |
| 4 |
| π |
| 4 |
考点:三角函数中的恒等变换应用,三角函数的最值
专题:三角函数的图像与性质
分析:由三角函数中的恒等变换应用化简函数解析式可得f(x)=
sin(2x-
),又x∈[-
,
],可得2x-
∈[-
,
],根据正弦函数的性质即可得解.
| 1 |
| 2 |
| π |
| 3 |
| π |
| 4 |
| π |
| 4 |
| π |
| 3 |
| 5π |
| 6 |
| π |
| 6 |
解答:
解:∵f(x)=cosx•sin(x+
)-
cos2x+
=cosx(
sinx+
cosx)-
cos2x+
=
sinxcosx+
cos2x-
cos2x+
=
sin2x-
×
+
=
sin(2x-
),
又∵x∈[-
,
],
∴2x-
∈[-
,
],
∴当2x-
=-
,即x=-
时,f(x)min=-
,
当2x-
=
,即x=
时,f(x)min=
,
故答案为:
、-
.
| π |
| 3 |
| 3 |
| ||
| 4 |
=cosx(
| 1 |
| 2 |
| ||
| 2 |
| 3 |
| ||
| 4 |
=
| 1 |
| 2 |
| ||
| 2 |
| 3 |
| ||
| 4 |
=
| 1 |
| 4 |
| ||
| 2 |
| 1+cos2x |
| 2 |
| ||
| 4 |
=
| 1 |
| 2 |
| π |
| 3 |
又∵x∈[-
| π |
| 4 |
| π |
| 4 |
∴2x-
| π |
| 3 |
| 5π |
| 6 |
| π |
| 6 |
∴当2x-
| π |
| 3 |
| π |
| 2 |
| π |
| 12 |
| 1 |
| 2 |
当2x-
| π |
| 3 |
| π |
| 6 |
| π |
| 4 |
| 1 |
| 4 |
故答案为:
| 1 |
| 4 |
| 1 |
| 2 |
点评:本题主要考查了三角函数中的恒等变换应用,三角函数的最值的解法,属于基本知识的考查.

练习册系列答案
相关题目
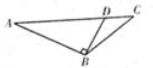
如图,在△ABC中,点D在AC上,AB⊥BD,BC=3
,BD=5,sin∠ABC=
,则CD的长为( )
| 3 |
2
| ||
| 5 |

A、
| ||
| B、4 | ||
C、2
| ||
| D、5 |
设二项式(x-
)4的展开式中常数项为A,则A=( )
| 1 | |||
|
| A、-6 | B、-4 | C、4 | D、6 |
数列{an}满足an+1=
,若a1=
,则a2015=( )
|
| 4 |
| 5 |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知函数f(x)=2sinx(
cosx-sinx)+1,若y=f(x-φ)为奇函数,则φ的一个值为( )
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
设函数f(x)=x|x-a|,若对?x1,x2∈[3,+∞),x1≠x2,不等式
>0恒成立,则实数a的取值范围是( )
| f(x1)-f(x2) |
| x1-x2 |
| A、(-∞,-3] |
| B、[-3,0) |
| C、(-∞,3] |
| D、(0,3] |
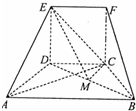 在如图所示的几何体中,四边形CDEF为正方形,ABCD为等腰梯形,AB∥CD,BD=2
在如图所示的几何体中,四边形CDEF为正方形,ABCD为等腰梯形,AB∥CD,BD=2


