题目内容
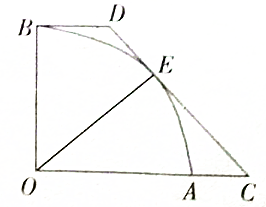 如图,扇形AOB的半径OA=2,∠AOB=
如图,扇形AOB的半径OA=2,∠AOB=| π |
| 2 |
 |
| AB |
考点:弧度制的应用
专题:计算题,三角函数的求值
分析:令∠C=α,易得∠EOD=∠BOD=
,OC=
,BD=2tan
,梯形面积最小,即OC+BD的和最小,即
+2tan
最小.
| α |
| 2 |
| 2 |
| sinα |
| α |
| 2 |
| 2 |
| sinα |
| α |
| 2 |
解答:
解:令∠C=α,易得∠EOD=∠BOD=
,OC=
,BD=2tan
,
梯形面积最小,即OC+BD的和最小,即
+2tan
最小.
令tan
=x,0<x<1,则原式化简=3x+
≥2
,
此时x=
,即BD=
,OC=
.
此时面积最小=
×2=2
.
| α |
| 2 |
| 2 |
| sinα |
| α |
| 2 |
梯形面积最小,即OC+BD的和最小,即
| 2 |
| sinα |
| α |
| 2 |
令tan
| α |
| 2 |
| 1 |
| x |
| 3 |
此时x=
| ||
| 3 |
2
| ||
| 3 |
4
| ||
| 3 |
此时面积最小=
| ||||||||
| 2 |
| 3 |
点评:本题考查三角函数知识的运用,考查学生的计算能力,考查基本不等式的运用,比较基础.

练习册系列答案
相关题目
已知定义在R上的函数y=f(x)满足f(x+2)=f(x),当-1<x≤1时,f(x)=x,若函数g(x)=f(x)-loga|x|至少有5个零点,则a的取值范围是( )
| A、(1,5) | ||
B、(0,
| ||
C、(0,
| ||
D、[
|
设a=log0.60.5,b=log2(log38),则( )
| A、b<1<a |
| B、a<b<1 |
| C、a<1<b |
| D、1<b<a |
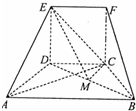 在如图所示的几何体中,四边形CDEF为正方形,ABCD为等腰梯形,AB∥CD,BD=2
在如图所示的几何体中,四边形CDEF为正方形,ABCD为等腰梯形,AB∥CD,BD=2