题目内容

若函数f（x）=a2x-4，g（x）=loga|x|（a＞0，且a≠1），且f（2）•g（2）＜0，则函数f（x），g（x）在同一坐标系中的大致图象是（　　）
A、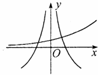
B、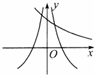
C、
D、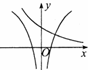
考点：函数的图象
专题：函数的性质及应用
分析：先由条件f（2）•g（2）＜0确定a的取值范围，然后利用指数函数和对数函数的性质去判断f（x），g（x）的图象．
解答： 解：由题意f（x）=a2x-4是指数型的，g（x）=loga|x|是对数型的且是一个偶函数，
由f（2）•g（2）＜0，可得出g（2）＜0，故loga2＜0，故0＜a＜1，由此特征可以确定C、D两选项不正确，
且f（x）=a2x-4是一个减函数，由此知A不对，B选项是正确答案
故选：B．
点评：本题主要考查了函数图象的识别和应用．判断函数图象要充分利用函数本身的性质，由f（2）•g（2）＜0确定a的取值范围，是解决本题的关键．
练习册系列答案
相关题目
设二项式（x-
1
3x
）4的展开式中常数项为A，则A=（　　）
A、-6B、-4C、4D、6
设函数f（x）=x|x-a|，若对?x1，x2∈[3，+∞），x1≠x2，不等式
f(x1)-f(x2)
x1-x2
＞0恒成立，则实数a的取值范围是（　　）
A、（-∞，-3]
B、[-3，0）
C、（-∞，3]
D、（0，3]
已知函数f（x）=
x+1，x∈[-1，0)
x2+1，x∈[0，1]
，则f（-x）的大致图象是（　　）
A、
B、
C、
D、
已知等比数列{an}的通项公式为an=3n-1，设数列{bn}满足对任意自然数n都有
b1
a1
+
b2
a2
+
b3
a3
+…+
bn
an
=2n+1恒成立．
①求数列{bn}的通项公式；
②求b1+b2+b3+…+b2005的值．
已知函数f（x）=2sin（2x+
π
6
）+a+1（a∈R，a为常数）．
（1）若x∈R，求f（x）的最小正周期；
（2）若f（x）在[-
π
6
，
π
6
]上最大值与最小值之和为3，求a的值．
y=sinx，x∈[-π，
π
6
]的单调区间
 
．
曲线y2=4ax与x=a围成的平面区域绕x轴旋转所得的旋转体的体积为
 
．
在△ABC中，已知∠A=30°，AB=
3
，BC=1，则AC的长为（　　）
A、2B、1C、2或1D、4

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网