题目内容
设函数f(x)=ax2+bx+1(a,b为常数,且a>0),f(-1)=0,且对任意实数x均有f(x)≥0.
(1)求函数f(x)的表达式;
(2)若g(x)=f(x)-kx(x∈[-2,2])是单调函数,求实数k的取值范围.
(1)求函数f(x)的表达式;
(2)若g(x)=f(x)-kx(x∈[-2,2])是单调函数,求实数k的取值范围.
考点:二次函数的性质
专题:计算题,函数的性质及应用
分析:(1)由f(-1)=0可得b=a+1;从而可得f(x)=ax2+(a+1)x+1,从而求得f(x)=x2+2x+1;
(2)由g(x)=x2+(2-k)x+1且g(x)在[-2,2]上是单调函数知
≤-2或
≥2;从而求解.
(2)由g(x)=x2+(2-k)x+1且g(x)在[-2,2]上是单调函数知
| k-2 |
| 2 |
| k-2 |
| 2 |
解答:
解:(1)∵f(-1)=0,∴b=a+1;
∴f(x)=ax2+(a+1)x+1,
又∵对任意实数x均有f(x)≥0,
∴△=(a-1)2≤0,
故a=1;
故f(x)=x2+2x+1;
(2)g(x)=x2+(2-k)x+1,
∵g(x)=f(x)-kx(x∈[-2,2])是单调函数,
∴
≤-2或
≥2;
故k≤-2或k≥6.
∴f(x)=ax2+(a+1)x+1,
又∵对任意实数x均有f(x)≥0,
∴△=(a-1)2≤0,
故a=1;
故f(x)=x2+2x+1;
(2)g(x)=x2+(2-k)x+1,
∵g(x)=f(x)-kx(x∈[-2,2])是单调函数,
∴
| k-2 |
| 2 |
| k-2 |
| 2 |
故k≤-2或k≥6.
点评:本题考查了二次函数的应用,属于基础题.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
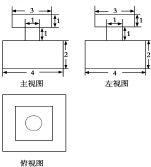
某品牌香水瓶的三视图如图(单位:cm),则该几何体的表面积为( )

A、(95-
| ||
B、(94-
| ||
C、(94+
| ||
D、(95+
|
曲线C的方程为
+
=1,其中m,n是将一枚骰子先后投掷两次所得点数,事件A=“方程
+
=1表示焦点在x轴上的椭圆”,那么P(A)=( )
| x2 |
| m2 |
| y2 |
| n2 |
| x2 |
| m2 |
| y2 |
| n2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
空间几何体的三视图如图所示,则该几何体的表面积和体积分别为( )


A、6+2
| ||
B、8+2
| ||
C、8+2
| ||
D、6+2
|
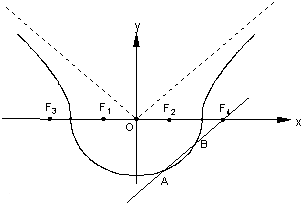 如图,曲线Γ由曲线
如图,曲线Γ由曲线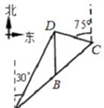 如图,B是线段AC上一点,经测量,点D位于点A的北偏东30°方向8km,位于点B的正北方向,位于点C的北偏西75°方向上,并且AB=5km.
如图,B是线段AC上一点,经测量,点D位于点A的北偏东30°方向8km,位于点B的正北方向,位于点C的北偏西75°方向上,并且AB=5km.