Question

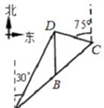如图，B是线段AC上一点，经测量，点D位于点A的北偏东30°方向8km，位于点B的正北方向，位于点C的北偏西75°方向上，并且AB=5km．
（1）求点B与D之间的距离（精确到0.1km）；
（2）求点C与D之间的距离（精确到0.1km）．
（参考数据：

3

=1.73，sin53°=0.80，cos38°=0.79）

Answer 1

考点：解三角形的实际应用

专题：综合题,解三角形

分析：（1）设BD=x，点D位于点A的北偏东30°方向，有∠ADB=30°，由余弦定理可求点B与D之间的距离；
（2）在△ABD中，由正弦定理得sin∠ABD，△CBD中，求出sin∠DCB，由正弦定理得CD．

解答： 解：（1）设BD=x，点D位于点A的北偏东30°方向，有∠ADB=30°，
由余弦定理可得25=64+x²-16xcos30°，解得x=4

3

±3，
∵4

3

+3＞8，∴x=4

3

-3≈3.9，
∴点B与D之间的距离约为3.9km；
（2）在△ABD中，由正弦定理得

8

sin∠ABD

=

5

sin30°

，
∴sin∠ABD=

4

5

，
∴sin∠CBD=

4

5

，∴∠CBD=53°，
△CBD中，sin∠DCB=sin128°=0.79，
由正弦定理得CD=sin∠DBC×

BD

sin∠DCB

≈4.0，
∴点C与D之间的距离约为4.0km．

点评：本题考查解三角形的实际应用，考查余弦定理、正弦定理，考查学生的计算能力，属于中档题．