Question

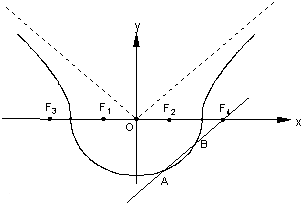如图，曲线Γ由曲线C1：

x2

a2

+

y2

b2

=1(a＞b＞0，y≤0)和曲线C2：

x2

a2

-

y2

b2

=1(y＞0)组成，其中点F₁，F₂为曲线C₁所在圆锥曲线的焦点，点F₃，F₄为曲线C₂所在圆锥曲线的焦点；
（1）若F₂（2，0），F₃（-6，0），求曲线Γ的方程；
（2）对于（1）中的曲线Γ，若过点F₄作直线l平行于曲线C₂的渐近线，交曲线C₁于点A、B，求三角形ABF₁的面积；
（3）如图，若直线l（不一定过F₄）平行于曲线C₂的渐近线，交曲线C₁于点A、B，求证：弦AB的中点M必在曲线C₂的另一条渐近线上．

Answer 1

考点：直线与圆锥曲线的综合问题

专题：圆锥曲线中的最值与范围问题

分析：（1）由F₂（2，0），F₃（-6，0），可得

a2+b2=36 a2-b2=4

，解得即可．
（2）由（1）知，曲线C₁：

x2

20

+

y2

16

=1，点F₄（6，0）．设直线l₁的方程为x=ny+6（n＞0）．与椭圆方程联立（5+4n²）y²+48ny+64=0，
△＞0，化为n²＞1．设C（x₃，y₃），D（x₄，y₄），利用根与系数的关系可得|y₃-y₄|=

(y3+y4)2-4y3y4

，利用S△CDF1=

1

2

|F1F4|•|y3-y4|与基本不等式的性质即可得出．
（3）曲线C₂的渐近线为y=±

b

a

x，如图，设直线l：y=

b

a

（x-m），与椭圆方程联立化为2x²-2mx+（m²-a²）=0，△＞0，由数形结合知a≤m≤

2

a．设点A（x₁，y₁），B（x₂，y₂），M（x₀，y₀），利用中点坐标公式与根与系数的关系即可证明即点M在直线y=-

b

a

x上．

解答： （1）解：∵F₂（2，0），F₃（-6，0），
∴

a2+b2=36 a2-b2=4

，
解得

a2=20 b2=16

，
则曲线Γ的方程为

x2

20

+

y2

16

=1和

x2

20

-

y2

16

=1．
（2）解：由（1）知，曲线C₁：

x2

20

+

y2

16

=1，点F₄（6，0）．
设直线l₁的方程为x=ny+6（n＞0）．联立

x2 20 + y2 16 =1 x=ny+6

，化为（5+4n²）y²+48ny+64=0，
△=（48n）²-4×64×（5+4n²）＞0，化为n²＞1．
设C（x₃，y₃），D（x₄，y₄），∴y₃+y₄=

-48n

5+4n2

，y3y4=

64

5+4n2

．
∴|y₃-y₄|=

(y3+y4)2-4y3y4

=

16 5 n2-1

5+4n2

，
S△CDF1=

1

2

|F1F4|•|y3-y4|=

1

2

×8×

16 5 n2-1

5+4n2

=

64 5 n2-1

5+4n2

，
令t=

n2-1

＞0，∴n²=t²+1，
∴SCDF1=

64 5 t

9+4t2

=

64 5

9 t +4t

≤

16 5

3

，当且仅当t=

3

2

，即n=

13

2

时等号成立．
∴n=

13

2

时，S△CDF1=

16 5

3

取得最大值．
（3）证明：曲线C₂的渐近线为y=±

b

a

x，
如图，设直线l：y=

b

a

（x-m），

y= b a (x-m) x2 a2 + y2 b2 =1

，化为2x²-2mx+（m²-a²）=0，
△=4m²-8（m²-a²）＞0，
解得-

2

a＜m＜

2

a．
又由数形结合知a≤m≤

2

a．
设点A（x₁，y₁），B（x₂，y₂），M（x₀，y₀），
则x₁+x₂=m，x₁x₂=

m2-a2

2

，
∴x₀=

x1+x2

2

=

m

2

，y0=

b

a

(x0-m)=-

b

a

×

m

2

．∴即点M在直线y=-

b

a

x上．

点评：本题考查了椭圆与双曲线的标准方程及其性质、直线与椭圆相交转化为方程联立可得根与系数的关系、弦长公式、三角形的面积计算公式、基本不等式的性质中点坐标公式，考查了推理能力与计算能力，属于难题．