题目内容
设f(x)是定义在[-1,1]上的奇函数,当x∈[-1,0)时,f(x)=
-
(a∈R).
(1)若f(x)在[0,1]上为单调增函数,求实数a的取值范围;
(2)求f(x)在[0,1]上的最大值.
| 1 |
| 4x |
| a |
| 2x |
(1)若f(x)在[0,1]上为单调增函数,求实数a的取值范围;
(2)求f(x)在[0,1]上的最大值.
考点:函数奇偶性的性质
专题:函数的性质及应用
分析:(1)根据奇函数在对称区间上具有相同的单调性,然后利用函数在x∈[-1,0)时为增函数得到含有a的不等式,即a>
=
+
,结合-1≤x1<x2<0即可求得a的范围;
(2)由f(x)是定义在[-1,1]上的奇函数求得a=1,得到函数在[0,1]上的解析式,换元后利用配方法求得函数的最大值.
| 2x1+2x2 |
| 2x12x2 |
| 1 |
| 2x1 |
| 1 |
| 2x2 |
(2)由f(x)是定义在[-1,1]上的奇函数求得a=1,得到函数在[0,1]上的解析式,换元后利用配方法求得函数的最大值.
解答:
解:(1)∵f(x)是定义在[-1,1]上的奇函数,且x∈[-1,0)时,f(x)=
-
(a∈R).
∴要使f(x)在[0,1]上为单调增函数,则x∈[-1,0)时,f(x)=
-
(a∈R)为得到增函数,
设-1≤x1<x2<0,
则f(x1)-f(x2)=
-
-
+
=
=
<0,
∴2x1+2x2<a•2x12x2,
即a>
=
+
,
∵-1≤x1<x2<0,
∴
,
∈(1,2],
∴
+
<4,
则a≥4;
(2)∵函数f(x)是定义在[-1,1]上的奇函数,
∴f(0)=
-
=0,解得a=1,
即当x∈[-1,0]时的解析式f(x)=
-
,
当x∈[0,1]时,-x∈[-1,0],
∴f(x)=-f(-x)=-(
-
)=2x-4x.
令t=2x(t∈[1,2])
则2x-4x=t-t2,
令y=t-t2(t∈[1,2]),
则可得当t=1时,y有最大值0,
∴f(x)在[0,1]上的最大值为0.
| 1 |
| 4x |
| a |
| 2x |
∴要使f(x)在[0,1]上为单调增函数,则x∈[-1,0)时,f(x)=
| 1 |
| 4x |
| a |
| 2x |
设-1≤x1<x2<0,
则f(x1)-f(x2)=
| 1 |
| 4x1 |
| a |
| 2x1 |
| 1 |
| 4x2 |
| a |
| 2x2 |
=
| 4x2-a•2x1•4x2-4x1+a•2x2•4x1 |
| 4x1•4x2 |
=
| (2x2-2x1)(2x1+2x2-a•2x12x2) |
| 4x14x2 |
∴2x1+2x2<a•2x12x2,
即a>
| 2x1+2x2 |
| 2x12x2 |
| 1 |
| 2x1 |
| 1 |
| 2x2 |
∵-1≤x1<x2<0,
∴
| 1 |
| 2x1 |
| 1 |
| 2x2 |
∴
| 1 |
| 2x1 |
| 1 |
| 2x2 |
则a≥4;
(2)∵函数f(x)是定义在[-1,1]上的奇函数,
∴f(0)=
| 1 |
| 40 |
| a |
| 20 |
即当x∈[-1,0]时的解析式f(x)=
| 1 |
| 4x |
| 1 |
| 2x |
当x∈[0,1]时,-x∈[-1,0],
∴f(x)=-f(-x)=-(
| 1 |
| 4-x |
| 1 |
| 2-x |
令t=2x(t∈[1,2])
则2x-4x=t-t2,
令y=t-t2(t∈[1,2]),
则可得当t=1时,y有最大值0,
∴f(x)在[0,1]上的最大值为0.
点评:本题考查了函数单调性和奇偶性的性质,训练了函数单调性的证明方法,考查了函数解析式的求法,训练了利用换元法和配方法求函数的最值,是中档题.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
下列语句中是命题的是( )
| A、正弦函数是周期函数吗? | ||||
B、sin60°=
| ||||
| C、5x2+x-6>0 | ||||
D、sin45°难道不等于
|
函数y=
的值域是 ( )
| x2-8x+15 |
| x2-x-6 |
| A、(-∞,1) | ||||
| B、(-∞,1)∪(1,+∞) | ||||
C、(-∞,-
| ||||
D、(-∞,-
|
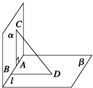 如图所示,在直二面角α-l-β中,A,B∈l,AC?α,AC⊥l,BD?β,BD⊥l,|AC|=6,|AB|=8,|BD|=24,则线段CD的长是( )
如图所示,在直二面角α-l-β中,A,B∈l,AC?α,AC⊥l,BD?β,BD⊥l,|AC|=6,|AB|=8,|BD|=24,则线段CD的长是( )