题目内容
在函数y=x3-9x的图象上，满足在该点处的切线倾斜角小于
，且横、纵坐标都为整数的个数是 ．
| π |
| 4 |
考点：利用导数研究函数的单调性
专题：计算题,导数的概念及应用
分析：根据倾斜角求出斜率的范围，设出切点坐标，利用导数的函数值就是该点的斜率，求出切点横坐标的范围，即可推出坐标为整数的点的个数．
解答：
解：∵切线倾斜角小于
，
∴斜率k∈[0，1）．
设切点为（x0，x03-9x0），则k=y′|x=x0=3x02-9，
∴0≤3x20-9＜1，即3≤x02＜
．
又∵x0∈Z，∴x0不存在．
故答案为：0
| π |
| 4 |
∴斜率k∈[0，1）．
设切点为（x0，x03-9x0），则k=y′|x=x0=3x02-9，
∴0≤3x20-9＜1，即3≤x02＜
| 10 |
| 3 |
又∵x0∈Z，∴x0不存在．
故答案为：0
点评：本题考查直线的斜率、导数的运算及几何意义，考查计算能力，逻辑思维能力，是基础题．
练习册系列答案
走进文言文系列答案
相关题目
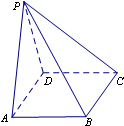如图，在四棱锥P-ABCD中，底面ABCD是正方形，侧面PAD⊥底面ABCD，且PA=PD=