题目内容
6.双曲线$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的一条渐近线被圆x2+y2-6x+5=0截得的弦长为2,则双曲线的离心率为$\frac{\sqrt{6}}{2}$.分析 求得双曲线的方程的渐近线方程,求得圆的圆心和半径,运用点到直线的距离公式和弦长公式,解方程可得a2=2b2,由a,b,c的关系和离心率公式,计算即可得到所求值.
解答 解:双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的渐近线方程为y=±$\frac{b}{a}$x,
圆x2+y2-6x+5=0即为(x-3)2+y2=4,
圆心为(3,0),半径为2,
圆心到渐近线的距离为d=$\frac{|3b|}{\sqrt{{a}^{2}+{b}^{2}}}$,
由弦长公式可得2=2$\sqrt{4-\frac{9{b}^{2}}{{a}^{2}+{b}^{2}}}$,
化简可得a2=2b2,
即有c2=a2+b2=$\frac{3}{2}$a2,
则e=$\frac{c}{a}$=$\frac{\sqrt{6}}{2}$.
故答案为:$\frac{\sqrt{6}}{2}$.
点评 本题考查双曲线的方程和性质,主要是渐近线方程的运用,考查直线和圆相交的弦长公式的运用,考查运算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
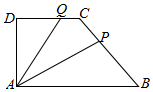 如图,在直角梯形ABCD中,AB∥CD,AB=2,AD=DC=1,P是线段BC上一动点,Q是线段DC上一动点,$\overrightarrow{DQ}=λ\overrightarrow{DC}$,$\overrightarrow{CP}=(1-λ)\overrightarrow{CB}$,若集合M=$\{x|x=\overrightarrow{AP}•\overrightarrow{AQ}\}$,N=$\left\{{x\left|{x=\frac{{{a^2}+{b^2}+1}}{3(a-b)},a>b,ab=1}\right.}\right\}$.则M∩N=[$\frac{2\sqrt{3}}{3}$,2].
如图,在直角梯形ABCD中,AB∥CD,AB=2,AD=DC=1,P是线段BC上一动点,Q是线段DC上一动点,$\overrightarrow{DQ}=λ\overrightarrow{DC}$,$\overrightarrow{CP}=(1-λ)\overrightarrow{CB}$,若集合M=$\{x|x=\overrightarrow{AP}•\overrightarrow{AQ}\}$,N=$\left\{{x\left|{x=\frac{{{a^2}+{b^2}+1}}{3(a-b)},a>b,ab=1}\right.}\right\}$.则M∩N=[$\frac{2\sqrt{3}}{3}$,2].