题目内容
16.设F1,F2是双曲线C:$\frac{{x}^{2}}{9}-\frac{{y}^{2}}{m}=1$的两个焦点,点P在C上,且$\overrightarrow{P{F}_{1}}$$•\overrightarrow{P{F}_{2}}$=0,若抛物线y2=16x的准线经过双曲线C的一个焦点,则|$\overrightarrow{P{F}_{1}}$|$•|\overrightarrow{P{F}_{2}}$|的值等于( )| A. | 2$\sqrt{2}$ | B. | 6 | C. | 14 | D. | 16 |
分析 求得抛物线的准线方程x=-4,可得双曲线的c=4,由向量垂直的条件和勾股定理,可得PF12+PF22=F1F22=4c2=64,①由双曲线的定义可得|PF1-PF2|=2a=6,②,运用平方相减即可得到所求值.
解答 解:抛物线y2=16x的准线为x=-4,
由题意可得双曲线的一个焦点为(-4,0),
即有c=4,
由$\overrightarrow{P{F}_{1}}$$•\overrightarrow{P{F}_{2}}$=0可得PF1⊥PF2,
由勾股定理可得,PF12+PF22=F1F22=4c2=64,①
由双曲线的定义可得|PF1-PF2|=2a=6,②
①-②2,可得2PF1•PF2=28,
即有|$\overrightarrow{P{F}_{1}}$|$•|\overrightarrow{P{F}_{2}}$|的值等于14.
故选:C.
点评 本题考查双曲线的定义、方程和性质,考查向量垂直的条件以及勾股定理,同时考查抛物线的方程和性质的运用,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.已知集合A={x||x|<1},B={x|x2-x≤0},则A∩B=( )
| A. | {x|-1≤x≤1} | B. | {x|0≤x≤1} | C. | {x|0<x≤1} | D. | {x|0≤x<1} |
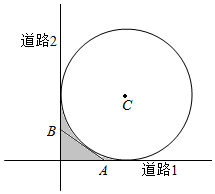 如图,某城市有一块半径为1(单位:百米)的圆形景观,圆心为C,有两条与圆形景观相切且互相垂直的道路.最初规划在拐角处(图中阴影部分)只有一块绿化地,后来有众多市民建议在绿化地上建一条小路,便于市民快捷地往返两条道路.规划部门采纳了此建议,决定在绿化地中增建一条与圆C相切的小道AB.问:A,B两点应选在何处可使得小道AB最短?
如图,某城市有一块半径为1(单位:百米)的圆形景观,圆心为C,有两条与圆形景观相切且互相垂直的道路.最初规划在拐角处(图中阴影部分)只有一块绿化地,后来有众多市民建议在绿化地上建一条小路,便于市民快捷地往返两条道路.规划部门采纳了此建议,决定在绿化地中增建一条与圆C相切的小道AB.问:A,B两点应选在何处可使得小道AB最短?