题目内容
16.设锐角△ABC的外接圆圆心为O,半径为25,弦AB=48,AC=40,则cos∠BAC的值为$\frac{3}{5}$,$\overrightarrow{OA}$$•\overrightarrow{OB}$+$\overrightarrow{OB}$$•\overrightarrow{OC}$+$\overrightarrow{OC}$$•\overrightarrow{OA}$=-877.分析 根据正弦定理求出sin∠ACB,sin∠ABC,利用两角和的余弦公式解出cos∠BAC,使用二倍角公式计算三个圆心角的余弦,代入平面向量的数量积公式计算.
解答 解:由正弦定理得$\frac{AB}{sin∠ACB}=\frac{AC}{sin∠ABC}=50$,
∴sin∠ACB=$\frac{24}{25}$,sin∠ABC=$\frac{4}{5}$.
∵△ABC是锐角三角形,
∴cos∠ACB=$\frac{7}{25}$,cos∠ABC=$\frac{3}{5}$.
∴cos(∠ACB+∠ABC)=$\frac{7}{25}×\frac{3}{5}-\frac{24}{25}×\frac{4}{5}$=-$\frac{3}{5}$.
∴cos∠BAC=-cos(∠ACB+∠ABC)=$\frac{3}{5}$.
由二倍角公式得:cos∠AOB=cos2∠ACB=2cos2∠ACB-1=-$\frac{527}{625}$.
cos∠BOC=cos2∠BAC=2cos2∠BAC-1=-$\frac{7}{25}$.
cos∠AOC=cos2∠ABC=1-2sin2∠ABC=-$\frac{7}{25}$.
∴$\overrightarrow{OA}•\overrightarrow{OB}$=25×25×cos∠AOB=-527.
$\overrightarrow{OB}•\overrightarrow{OC}$=25×25×cos∠BOC=-175,
$\overrightarrow{OA}•\overrightarrow{OC}$=25×25×cos∠AOC=-175.
∴$\overrightarrow{OA}$$•\overrightarrow{OB}$+$\overrightarrow{OB}$$•\overrightarrow{OC}$+$\overrightarrow{OC}$$•\overrightarrow{OA}$=-527-175-175=-877.
故答案为:$\frac{3}{5}$,-877.
点评 本题考查了正弦定理,二倍角公式,平面向量的数量积运算,属于中档题.

 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案| A. | λ=0 | B. | $\overrightarrow{{l}_{2}}$=$\overrightarrow{0}$ | C. | $\overrightarrow{{l}_{1}}$∥$\overrightarrow{{l}_{2}}$ | D. | $\overrightarrow{{l}_{2}}$=$\overrightarrow{0}$或λ=0 |
| A. | -$\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | -$\frac{1}{2}$或1 | D. | $\frac{1}{2}$或0 |
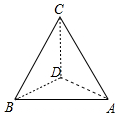 如图,为了估测某塔的高度,在同一水平面的A,B两点处进行测量,在点A处测得塔顶C在西偏北20°的方向上,仰角为60°;在点B处测得塔顶C在东偏北40°的方向上,仰角为30°.若A,B两点相距130m,则塔的高度CD=10$\sqrt{39}$ m.
如图,为了估测某塔的高度,在同一水平面的A,B两点处进行测量,在点A处测得塔顶C在西偏北20°的方向上,仰角为60°;在点B处测得塔顶C在东偏北40°的方向上,仰角为30°.若A,B两点相距130m,则塔的高度CD=10$\sqrt{39}$ m.