题目内容
14.已知M点是△ABC的重心,若以AB为直径的圆恰好经过点M,则$\frac{tanC}{tanA}$+$\frac{tanC}{tanB}$的值为$\frac{1}{2}$.分析 首先根据三角形的重心性质及直角三角形的斜边的中线等于斜边的一半,得到CD=$\frac{3}{2}$AB,再应用余弦定理推出AC2+BC2=5AB2,将$\frac{tanC}{tanA}$+$\frac{tanC}{tanB}$应用三角恒等变换公式化简得$\frac{si{n}^{2}C}{sinAsinBcosC}$,然后运用正弦定理和余弦定理,结合前面的结论,即可求值得解.
解答 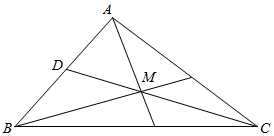 解:如图,连接CM,延长交AB于D,
解:如图,连接CM,延长交AB于D,
由于M为重心,故D为中点,
∵AM⊥BM,∴DM=$\frac{1}{2}$AB,
由重心的性质得,CD=3DM,即CD=$\frac{3}{2}$AB,
由余弦定理得,AC2=AD2+CD2-2AD•CD•cos∠ADC,
BC2=BD2+CD2-2BD•CD•cos∠BDC,
∵∠ADC+∠BDC=π,AD=BD,
∴AC2+BC2=2AD2+2CD2,
∴AC2+BC2=$\frac{1}{2}$AB2+$\frac{9}{2}$AB2=5AB2,
∴$\frac{tanC}{tanA}$+$\frac{tanC}{tanB}$=$\frac{sinC(cosAsinB+cosBsinA)}{sinAsinBcosC}$=$\frac{si{n}^{2}C}{sinAsinBcosC}$=$\frac{A{B}^{2}}{BC•AC•cosC}$=$\frac{A{B}^{2}}{\frac{B{C}^{2}+A{C}^{2}-A{B}^{2}}{2}}$=$\frac{2A{B}^{2}}{5A{B}^{2}-A{B}^{2}}$=$\frac{1}{2}$.
故答案为:$\frac{1}{2}$.
点评 本题主要考查解三角形中的正弦定理与余弦定理及应用,考查三角恒等变换,三角形的重心的性质,考查运算能力,有一定的难度.

 名校课堂系列答案
名校课堂系列答案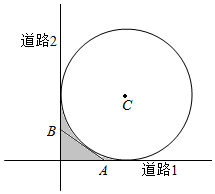 如图,某城市有一块半径为1(单位:百米)的圆形景观,圆心为C,有两条与圆形景观相切且互相垂直的道路.最初规划在拐角处(图中阴影部分)只有一块绿化地,后来有众多市民建议在绿化地上建一条小路,便于市民快捷地往返两条道路.规划部门采纳了此建议,决定在绿化地中增建一条与圆C相切的小道AB.问:A,B两点应选在何处可使得小道AB最短?
如图,某城市有一块半径为1(单位:百米)的圆形景观,圆心为C,有两条与圆形景观相切且互相垂直的道路.最初规划在拐角处(图中阴影部分)只有一块绿化地,后来有众多市民建议在绿化地上建一条小路,便于市民快捷地往返两条道路.规划部门采纳了此建议,决定在绿化地中增建一条与圆C相切的小道AB.问:A,B两点应选在何处可使得小道AB最短?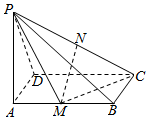 如图,已知PA⊥矩形ABCD所在的平面,M、N分别为AB、PC的中点,∠PDA=45°.
如图,已知PA⊥矩形ABCD所在的平面,M、N分别为AB、PC的中点,∠PDA=45°.