题目内容
18.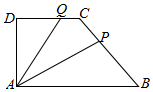 如图,在直角梯形ABCD中,AB∥CD,AB=2,AD=DC=1,P是线段BC上一动点,Q是线段DC上一动点,$\overrightarrow{DQ}=λ\overrightarrow{DC}$,$\overrightarrow{CP}=(1-λ)\overrightarrow{CB}$,若集合M=$\{x|x=\overrightarrow{AP}•\overrightarrow{AQ}\}$,N=$\left\{{x\left|{x=\frac{{{a^2}+{b^2}+1}}{3(a-b)},a>b,ab=1}\right.}\right\}$.则M∩N=[$\frac{2\sqrt{3}}{3}$,2].
如图,在直角梯形ABCD中,AB∥CD,AB=2,AD=DC=1,P是线段BC上一动点,Q是线段DC上一动点,$\overrightarrow{DQ}=λ\overrightarrow{DC}$,$\overrightarrow{CP}=(1-λ)\overrightarrow{CB}$,若集合M=$\{x|x=\overrightarrow{AP}•\overrightarrow{AQ}\}$,N=$\left\{{x\left|{x=\frac{{{a^2}+{b^2}+1}}{3(a-b)},a>b,ab=1}\right.}\right\}$.则M∩N=[$\frac{2\sqrt{3}}{3}$,2].
分析 用$\overrightarrow{AB},\overrightarrow{AD}$表示$\overrightarrow{AP},\overrightarrow{AQ}$,根据λ的范围求出$\overrightarrow{AP}•\overrightarrow{AQ}$的范围,即M的范围,根据基本不等式求出N的范围,得出M∩N.
解答 解:∵$\overrightarrow{DQ}=λ\overrightarrow{DC}$,∴0≤λ≤1.
$\overrightarrow{CB}=\overrightarrow{CD}+\overrightarrow{DA}+\overrightarrow{AB}$=$\frac{1}{2}\overrightarrow{AB}-\overrightarrow{AD}$.
$\overrightarrow{AP}$=$\overrightarrow{AD}+\overrightarrow{DC}+\overrightarrow{CP}$=$\overrightarrow{AD}+\frac{λ}{2}\overrightarrow{AB}+(1-λ)$($\frac{1}{2}\overrightarrow{AB}-\overrightarrow{AD}$)=$\frac{1}{2}\overrightarrow{AB}+λ\overrightarrow{AD}$.
$\overrightarrow{AQ}$=$\overrightarrow{AD}+\overrightarrow{DQ}$=$\frac{λ}{2}\overrightarrow{AB}+\overrightarrow{AD}$.
∴$\overrightarrow{AP}•\overrightarrow{AQ}$=($\frac{1}{2}\overrightarrow{AB}+λ\overrightarrow{AD}$)•($\frac{λ}{2}\overrightarrow{AB}+\overrightarrow{AD}$)=$\frac{λ}{4}{\overrightarrow{AB}}^{2}$+$λ{\overrightarrow{AD}}^{2}$=2λ.
∴M=$\{x|x=\overrightarrow{AP}•\overrightarrow{AQ}\}$=[0,2].
∵a>b,ab=1,
∴a-b>0,
$\frac{{a}^{2}+{b}^{2}+1}{3(a-b)}$=$\frac{(a-b)^{2}+2ab+1}{3(a-b)}$=$\frac{a-b}{3}+\frac{1}{a-b}$≥2$\sqrt{\frac{1}{3}}$=$\frac{2\sqrt{3}}{3}$.
∴N={x|x=$\frac{{a}^{2}+{b}^{2}+1}{3(a-b)}$,a>b,ab=1}=[$\frac{2\sqrt{3}}{3}$,+∞).
∴M∩N=[$\frac{2\sqrt{3}}{3}$,2].
故答案为:$[{\frac{{2\sqrt{3}}}{3},2}]$.
点评 本题考查了平面向量线性运算的几何意义,向量的数量积运算,基本不等式及集合运算,属于中档题.

| A. | $\frac{4π}{3}$ | B. | $\frac{2π}{3}$ | C. | $\frac{π}{3}$ | D. | -$\frac{π}{3}$ |
| A. | λ=0 | B. | $\overrightarrow{{l}_{2}}$=$\overrightarrow{0}$ | C. | $\overrightarrow{{l}_{1}}$∥$\overrightarrow{{l}_{2}}$ | D. | $\overrightarrow{{l}_{2}}$=$\overrightarrow{0}$或λ=0 |