题目内容
已知函数f(x)=ax+
在(1,f(1))处的切线斜率为1,g(x)=lnx-f(x),
(1)求a,b之间的关系式;
(2)若关于x的不等式g(x)+ax>0对任意x∈(0,+∞)恒成立,求实数a的取值范围;
(3)已知a>0,且a≠
,求函数y=g(x)在[1,+∞)上的最大值(用a表示).
| b |
| x |
(1)求a,b之间的关系式;
(2)若关于x的不等式g(x)+ax>0对任意x∈(0,+∞)恒成立,求实数a的取值范围;
(3)已知a>0,且a≠
| 1 |
| 2 |
考点:利用导数研究函数的极值,利用导数研究函数的单调性
专题:导数的概念及应用,导数的综合应用
分析:(1)由已知函数f(x)=ax+
在(1,f(1))处的切线斜率为1,可得f′(1)=a-b=1;
(2)若g(x)+ax=lnx-
>0恒成立,即lnx>
恒成立,即b<x•lnx恒成立,构造函数h(x)=x•lnx,利用导数法,求出函数的最小值,可得答案.
(3)g′(x)=0,则x=1,或x=
,由a>0,且a≠
,分当0<a<
时和当a>
时两种情况分析函数的单调性进而可和函数y=g(x)在[1,+∞)上的最大值.
| b |
| x |
(2)若g(x)+ax=lnx-
| b |
| x |
| b |
| x |
(3)g′(x)=0,则x=1,或x=
| 1-a |
| a |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:
解:(1)∵f(x)=ax+
,
∴f′(x)=a-
,
又∵f(x)=ax+
在(1,f(1))处的切线斜率为1,
∴f′(1)=a-b=1,
(2)∵g(x)=lnx-f(x)=lnx-ax-
,
若g(x)+ax=lnx-
>0恒成立,
即lnx>
恒成立,
即b<x•lnx恒成立,
令h(x)=x•lnx,
则h′(x)=lnx+1,
令h′(x)=0,则x=
,
当x∈(0,
)时,h′(x)<0,此时h(x)单调递减;
当x∈(
,+∞)时,h′(x)>0,此时h(x)单调递增;
故当x=
时,h(x)=x•lnx取最小值-
,
故b<-
,
即a-1<-
,
即a<1-
,
即实数a的取值范围为(-∞,1-
),
(3)∵g(x)=lnx-f(x)=lnx-ax-
,
∴g′(x)=
-a+
=
=
=
,
令g′(x)=0,则x=1,或x=
∵a>0,且a≠
,
当0<a<
时,
>1,
当x∈[1,
)时,g′(x)>0,g(x)为增函数,当x∈(
,+∞)时,g′(x)<0,g(x)为减函数,
故当x=
时,g(x)取最大值ln
-1,
当a>
时,
<1,
当x∈[1,+∞)时,g′(x)<0,g(x)为减函数,
故当x=1时,g(x)取最大值1-2a
| b |
| x |
∴f′(x)=a-
| b |
| x2 |
又∵f(x)=ax+
| b |
| x |
∴f′(1)=a-b=1,
(2)∵g(x)=lnx-f(x)=lnx-ax-
| b |
| x |
若g(x)+ax=lnx-
| b |
| x |
即lnx>
| b |
| x |
即b<x•lnx恒成立,
令h(x)=x•lnx,
则h′(x)=lnx+1,
令h′(x)=0,则x=
| 1 |
| e |
当x∈(0,
| 1 |
| e |
当x∈(
| 1 |
| e |
故当x=
| 1 |
| e |
| 1 |
| e |
故b<-
| 1 |
| e |
即a-1<-
| 1 |
| e |
即a<1-
| 1 |
| e |
即实数a的取值范围为(-∞,1-
| 1 |
| e |
(3)∵g(x)=lnx-f(x)=lnx-ax-
| b |
| x |
∴g′(x)=
| 1 |
| x |
| b |
| x2 |
| -ax2+x+b |
| x2 |
| -ax2+x+a-1 |
| x2 |
| (ax+a-1)(-x+1) |
| x2 |
令g′(x)=0,则x=1,或x=
| 1-a |
| a |
∵a>0,且a≠
| 1 |
| 2 |
当0<a<
| 1 |
| 2 |
| 1-a |
| a |
当x∈[1,
| 1-a |
| a |
| 1-a |
| a |
故当x=
| 1-a |
| a |
| 1-a |
| a |
当a>
| 1 |
| 2 |
| 1-a |
| a |
当x∈[1,+∞)时,g′(x)<0,g(x)为减函数,
故当x=1时,g(x)取最大值1-2a
点评:本题考查的知识点是利用导数研究函数的极值,利用函数研究函数的单调性,利用导数研究函数的最值,是导数部分的综合应用,难度中档.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
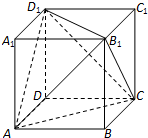 如图,已知正方体ABCD-A1B1C1D1的棱长为1.
如图,已知正方体ABCD-A1B1C1D1的棱长为1.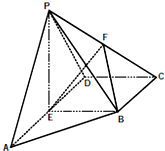 如图,在四棱锥P-ABCD中,E为AD的中点,F为PC的中点,PE⊥平面ABCD,AD∥BC,AD⊥CD,且BC=CD=
如图,在四棱锥P-ABCD中,E为AD的中点,F为PC的中点,PE⊥平面ABCD,AD∥BC,AD⊥CD,且BC=CD=