题目内容
设a∈R,函数f(x)=ax3-3x2.
(Ⅰ)若x=2是函数y=f(x)的极值点,求a的值;
(Ⅱ)设函数g(x)=f(x)+f′(x),若g(x)≤0对一切x∈(0,2]都成立,求a的取值范围.
(Ⅰ)若x=2是函数y=f(x)的极值点,求a的值;
(Ⅱ)设函数g(x)=f(x)+f′(x),若g(x)≤0对一切x∈(0,2]都成立,求a的取值范围.
考点:利用导数研究函数的极值,导数的运算,利用导数求闭区间上函数的最值
专题:导数的综合应用
分析:(Ⅰ)f′(x)=3ax2-6x=3x(ax-2).由f′(2)=0,得a=1.经验证,当a=1时,x=2是函数y=f(x)的极值点.
(Ⅱ)由题设,g(x)=ax3+3(a-1)x2-6x.由ax3+3(a-1)x2-6x≤0对一切x∈(0,2]都成立,令φ(x)=
,x∈(0,2],则a≤φ(x)min由φ′(x)=
<0,可知φ(x)=
在x∈(0,2]上单调递减,从而φ(x)min=φ(2)=
,静儿求出a的取值范围是(-∞,
].
(Ⅱ)由题设,g(x)=ax3+3(a-1)x2-6x.由ax3+3(a-1)x2-6x≤0对一切x∈(0,2]都成立,令φ(x)=
| 3x+6 |
| x2+3x |
| -3(x+2)2-6 |
| (x2+3x)2 |
| 3x+6 |
| x2+3x |
| 6 |
| 5 |
| 6 |
| 5 |
解答:
解:(Ⅰ)f′(x)=3ax2-6x=3x(ax-2).
∵x=2是函数y=f(x)的极值点,
∴f′(2)=0,即6(2a-2)=0,
∴a=1.
经验证,当a=1时,x=2是函数y=f(x)的极值点.
(Ⅱ)由题设,g(x)=ax3+3(a-1)x2-6x.
ax3+3(a-1)x2-6x≤0对一切x∈(0,2]都成立,
即a≤
对一切x∈(0,2]都成立.
令φ(x)=
,x∈(0,2],则a≤φ(x)min
由φ′(x)=
<0,
可知φ(x)=
在x∈(0,2]上单调递减,
∴φ(x)min=φ(2)=
,
故a的取值范围是(-∞,
].
∵x=2是函数y=f(x)的极值点,
∴f′(2)=0,即6(2a-2)=0,
∴a=1.
经验证,当a=1时,x=2是函数y=f(x)的极值点.
(Ⅱ)由题设,g(x)=ax3+3(a-1)x2-6x.
ax3+3(a-1)x2-6x≤0对一切x∈(0,2]都成立,
即a≤
| 3x+6 |
| x2+3x |
令φ(x)=
| 3x+6 |
| x2+3x |
由φ′(x)=
| -3(x+2)2-6 |
| (x2+3x)2 |
可知φ(x)=
| 3x+6 |
| x2+3x |
∴φ(x)min=φ(2)=
| 6 |
| 5 |
故a的取值范围是(-∞,
| 6 |
| 5 |
点评:本题考察了函数的单调性,函数的极值,最值问题,导数的应用,是一道综合题.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
在区间[1,3]上任取一数,则这个数大于等于1.5的概率为( )
| A、0.25 | B、0.5 |
| C、0.6 | D、0.75 |
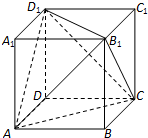 如图,已知正方体ABCD-A1B1C1D1的棱长为1.
如图,已知正方体ABCD-A1B1C1D1的棱长为1.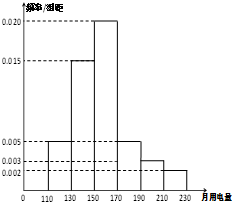 2013年第三季度,国家电网决定对城镇居民民用电计费标准做出调整,并根据用电情况将居民分为三类:第一类的用电区间在(0,170],第二类在(170,260],第三类在(260,+∞)(单位:千瓦时).某小区共有1000户居民,现对他们的用电情况进行调查,得到频率分布直方图如图所示.
2013年第三季度,国家电网决定对城镇居民民用电计费标准做出调整,并根据用电情况将居民分为三类:第一类的用电区间在(0,170],第二类在(170,260],第三类在(260,+∞)(单位:千瓦时).某小区共有1000户居民,现对他们的用电情况进行调查,得到频率分布直方图如图所示.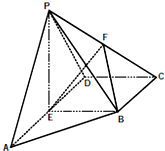 如图,在四棱锥P-ABCD中,E为AD的中点,F为PC的中点,PE⊥平面ABCD,AD∥BC,AD⊥CD,且BC=CD=
如图,在四棱锥P-ABCD中,E为AD的中点,F为PC的中点,PE⊥平面ABCD,AD∥BC,AD⊥CD,且BC=CD=