题目内容
4.在△ABC中,a,b,c分别是A,B,C的对边,且$\sqrt{2}$sinA=$\sqrt{3cosA}$.(1)若a2-c2=b2-mbc,求实数m的值;
(2)若a=2,求△ABC面积的最大值.
分析 (1)将$\sqrt{2}$sinA=$\sqrt{3cosA}$.两边平方,可解得:cosA=$\frac{1}{2}$,又0$<A<\frac{π}{2}$,可求A,利用已知及余弦定理即可得解m的值.
(2)利用余弦定理及基本不等式可得bc=b2+c2-a2≥2bc-a2,(当且仅当b=c时取等号)即bc≤a2,利用三角形面积公式即可得解.
解答 解:(1)将$\sqrt{2}$sinA=$\sqrt{3cosA}$.两边平方,可得:2sin2A=3cosA,
即:(2cosA-1)(cosA+2)=0,解得:cosA=$\frac{1}{2}$,
∵0$<A<\frac{π}{2}$,
∴A=60°.
∵a2-c2=b2-mbc,可以变形可得:$\frac{{b}^{2}+{c}^{2}-{a}^{2}}{2bc}$=$\frac{m}{2}$,即cosA=$\frac{m}{2}=\frac{1}{2}$,
∴m=1.…6分
(2)∵cosA=$\frac{{b}^{2}+{c}^{2}-{a}^{2}}{2bc}$=$\frac{1}{2}$,
∴bc=b2+c2-a2≥2bc-a2,(当且仅当b=c时取等号)即bc≤a2,
∴S△ABC=$\frac{bc}{2}$sinA≤$\frac{{a}^{2}}{2}$×$\frac{\sqrt{3}}{2}$=$\sqrt{3}$,
∴△ABC的面积的最大值为$\sqrt{3}$.…12分
点评 本题主要考查了余弦定理,基本不等式在解三角形中的应用,考查计算能力和转化思想,属于中档题.

练习册系列答案
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目
9.某产品的广告费x(万元)与销售额y(万元)的统计数据如表:
根据如表可知回归直线方程$\stackrel{∧}{y}$=bx+$\stackrel{∧}{a}$中的b为7,据此模型,若广告费用为10万元,则预计销售额为( )万元.
| 广告费x(万元) | 3 | 4 | 5 | 6 |
| 销售额y(万元) | 25 | 30 | 40 | 45 |
| A. | 72.5 | B. | 73.5 | C. | 74.5 | D. | 75.5 |
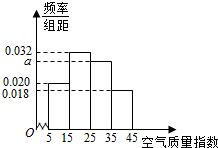 进入冬季以来,我国北方地区的雾霾天气持续出现,极大的影响了人们的健康和出行,我市环保局对该市2015年进行为期一年的空气质量监测,得到每天的空气质量指数,从中随机抽取50个作为样本进行分析报告,样本数据分组区间为(5,15],(15,25],(25,35],(35,45],由此得到样本的空气质量指数频率分布直方图,如图.
进入冬季以来,我国北方地区的雾霾天气持续出现,极大的影响了人们的健康和出行,我市环保局对该市2015年进行为期一年的空气质量监测,得到每天的空气质量指数,从中随机抽取50个作为样本进行分析报告,样本数据分组区间为(5,15],(15,25],(25,35],(35,45],由此得到样本的空气质量指数频率分布直方图,如图. 有60m长的钢材,要制作如图所示的窗框:
有60m长的钢材,要制作如图所示的窗框: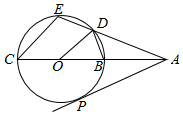 如图,已知圆O的内接四边形BCED,BC为圆O的直径,BC=2,延长CB,ED交于A点,使得∠DOB=∠ECA,过A作圆O的切线,切点为P,
如图,已知圆O的内接四边形BCED,BC为圆O的直径,BC=2,延长CB,ED交于A点,使得∠DOB=∠ECA,过A作圆O的切线,切点为P,