题目内容
16．直线y=x被圆x2+y2-2y-3=0截得的弦长等于$\sqrt{14}$．分析 由圆的方程求出圆心和半径，求出圆心到直线y=x的距离d的值，再根据弦长公式求得弦长．
解答 解：圆x2+y2-2y-3=0即x2+（y-1）2=4，表示以C（0，1）为圆心，半径等于2的圆．
由于圆心到直线y=x的距离为d=$\frac{1}{\sqrt{2}}$，
故弦长为2$\sqrt{4-\frac{1}{2}}$=$\sqrt{14}$，
故答案为：$\sqrt{14}$．
点评 本题主要考查直线和圆相交的性质，点到直线的距离公式，弦长公式的应用，属于中档题．
练习册系列答案
孟建平错题本系列答案
超能学典应用题题卡系列答案
相关题目
7．某高校“统计初步”课程的教师为了检验主修统计专业是否与性别有关系，随机调查了选该课的学生人数情况，具体数据如表，则大约有99.5%的把握认为主修统计专业与性别有关系．参考公式：${Χ^2}=\frac{{n{{（ad-bc）}^2}}}{（a+b）（c+d）（a+c）（b+d）}$．
| 非统计专业 | 统计专业 | |
| 男 | 15 | 10 |
| 女 | 5 | 20 |
| P（Χ2＞x0） | 0.025 | 0.010 | 0.005 | 0.001 |
| x0 | 5.024 | 6.635 | 7.879 | 10.828 |
5．（x3-$\frac{2}{x}$）4的展开式中的常数项为（ ）
| A． | 32 | B． | 64 | C． | -32 | D． | -64 |
6．在平面四边形ABCD中，∠A=∠B=60°，∠C=75°，BC=2，则AB的取值范围是（ ）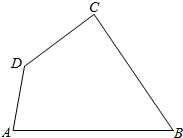
| A． | （$\sqrt{3}$-1，2） | B． | （2，$\sqrt{3}$+1） | C． | （$\sqrt{3}$-1，$\sqrt{3}$+1） | D． | （2，4） |