题目内容
4.四棱锥A-BCDE,底面BCDE为梯形,EB∥DC,DC⊥平面ABC,AC=BC=EB=2DC,∠ACB=90°,AD与平面ABE所成角的正弦值为( )| A. | $\frac{\sqrt{10}}{5}$ | B. | $\frac{\sqrt{5}}{5}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
分析 利用线面、面面垂直的判定和性质定理得到CQ⊥平面ABE,再利用DP∥CQ可证明DP⊥平面ABE,从而得到∠DAP是所求的线面角.
解答 解:设P,Q分别为AE,AB的中点,
则PQ∥EB,且EB=2PQ,
∴四边形DCQP是平行四边形,
∴DP∥CQ
设在△ABC中,AC=BC=2a,AQ=BQ,
∴CQ⊥AB.
而DC⊥平面ABC,EB∥DC,
∴EB⊥平面ABC.
而EB?平面ABE,
∴平面ABE⊥平面ABC,
∴CQ⊥平面ABE
∴DP⊥平面ABE,
∴直线AD在平面ABE内的射影是AP,
∴直线AD与平面ABE所成角是∠DAP.
在Rt△APD中,AD=$\sqrt{{AC}^{2}+{DC}^{2}}$=$\sqrt{5}$a,
DP=CQ=2asin∠CAQ=2sin30°=a.
∴sin∠DAP=$\frac{DP}{AD}$=$\frac{a}{\sqrt{5}a}$=$\frac{\sqrt{5}}{5}$,
故选:B.
点评 本题考查平面与平面垂直的证明,考查直线与平面所成角的正弦值的求法.解题时要认真审题,合理地化空间问题为平面问题,注意空间思维能力和推理能力的培养

练习册系列答案
相关题目
15.定义在R上的奇函数f(x),当x∈(-∞,0)时xf(x)递减,若a=3f(3),b=(logπ3)•f(logπ3),c=-2f(-2),则a,b,c的大小关系( )
| A. | a<c<b | B. | a<b<c | C. | c<a<b | D. | b<c<a |
12.设p:“$\frac{a-1}{a-2}$≥0”,q:“圆x2+y2=a2(a>0)与直线3x+4y-5=0相交且与圆(x+3)2+(y+4)2=9外离”,则¬p是q的( )条件.
| A. | 充分不必要 | B. | 必要不充分 | ||
| C. | 充要 | D. | 既不充分也不必要 |
14.已知等比数列{an}的前n项和为Sn,则下列一定成立的是( )
| A. | 若a4>0,则a2016<0 | B. | 若a5>0,则a2015<0 | ||
| C. | 若a4>0,则S2016>0 | D. | 若a5>0,则S2015>0 |
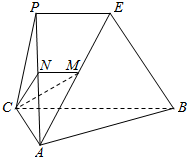 如图,平面PAC⊥平面ABC,AC⊥BC,PE∥CB,M是AE的中点.
如图,平面PAC⊥平面ABC,AC⊥BC,PE∥CB,M是AE的中点.