题目内容

19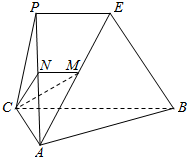．如图，平面PAC⊥平面ABC，AC⊥BC，PE∥CB，M是AE的中点．
（1）若N是PA的中点，求证：平面CMN⊥平面PAC；
（2）若MN∥平面ABC，求证：N是PA的中点．

分析 （1）由已知得BC⊥平面PAC，MN∥PE，从而MN∥BC，进而MN⊥平面PAC，由此能证明CMN⊥平面PAC．
（2）由MN∥平面ABC，PE∥CB，得MN∥PE，由此能证明N是PA的中点．

解答 证明：（1）∵平面PAC⊥平面ABC，AC⊥BC，
∴BC⊥平面PAC，
∵PE∥CB，M是AE的中点，N是PA的中点，
∴MN∥PE，∴MN∥BC，
∴MN⊥平面PAC，
∵MN?平面CMN，∴平面CMN⊥平面PAC．
（2）∵MN∥平面ABC，PE∥CB，
∴MN∥PE，
∵M是AE的中点，∴N是PA的中点．

点评 本题考查面面垂直的证明，考查点是线段中点的证明，是中档题，解题时要认真审题，注意空间思维能力的培养．

练习册系列答案
相关题目
9．已知函数f（x）满足f（-x）=f（x），且f（x+2）=f（x）+f（2），当x∈[0，1]时，f（x）=x，那么在区间[-1，3]内，关于x的方程f（x）=kx+k+1（k∈R）且k≠-1恰有4个不同的根，则k的取值范围是（$-\frac{1}{3}$，0）．
10．已知函数f（x）=ex
（Ⅰ）证明：当x≠0时，（1-x）f（x）＜1；
（Ⅱ）证明：当a≠b时，$\frac{f（a）-f（b）}{a-b}$＜$\frac{f（a）+f（b）}{2}$．
7．已知圆O：x2+y2=1，点P（-1，2），过点P作圆O的切线，求切线方程．
14．已知集合A={-1，0，1}，B={0，a，2}，若A∩B={-1，0}，则a=-1．
4．四棱锥A-BCDE，底面BCDE为梯形，EB∥DC，DC⊥平面ABC，AC=BC=EB=2DC，∠ACB=90°，AD与平面ABE所成角的正弦值为（　　）
A．$\frac{\sqrt{10}}{5}$B．$\frac{\sqrt{5}}{5}$C．$\frac{1}{2}$D．$\frac{\sqrt{3}}{2}$
11．已知f（x）是定义在[-2，2]上的奇函数，且g（x）=f（x）+6，f（-2）=4，当a，b∈[-2，2]，a+b≠0时，恒有（a+b）[f（a）+f（b）]＜0成立．
（Ⅰ）求g（2）的值；
（Ⅱ）判断f（x）在[-2，2]上的单调性（不用证明）；
（Ⅲ）若g（x）≤m2-2km+2对所有的k∈[-1，1]恒成立，求实数m的取值范围．
8．设复数z1，z2在复平面内对应的点关于原点对称，若z1=2-3i（i为虚数单位），则z2=（　　）
A．-2+3iB．-2-3iC．2+3iD．2-3i
9．已知函数f（x）=ax．
（I）若a=2时，关于x的方程f（x）+f（1-x）-m=0在区间[1，2]内有解，求实数m的取值范围；
（Ⅱ）若a＞0，且a≠1，函数g（x）=f（2x）+2f（x）-1在[-1，1]上的最大值是14，求a的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网