题目内容
14.设变量x,y满足约束条件$\left\{\begin{array}{l}{x-y≤1}\\{x+y≥2}\\{y≤2}\end{array}\right.$,则目标函数z=x2+y2的取值范围是[2,13].分析 由约束条件作出可行域,z=x2+y2可看作可行域内的点到原点的距离的平方,数形结合求得目标函数z=x2+y2的取值范围.
解答 解:由约束条件$\left\{\begin{array}{l}{x-y≤1}\\{x+y≥2}\\{y≤2}\end{array}\right.$作出可行域如图,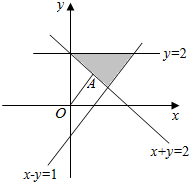
联立$\left\{\begin{array}{l}{y=2}\\{x-y=1}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=3}\\{y=2}\end{array}\right.$.
z=x2+y2可看作可行域内的点到原点的距离的平方,从而有
${z}_{min}=(\frac{|0+0-2|}{\sqrt{{1}^{2}+{1}^{2}}})^{2}=2$,${z}_{max}={3}^{2}+{2}^{2}=13$,
∴z∈[2,13].
故答案为:[2,13].
点评 本题考查简单的线性规划,考查了数形结合的解题思想方法,是中档题.

练习册系列答案
相关题目
5.某学生参加3个项目的体能测试,若该生第一个项目测试过关的概率为$\frac{4}{5}$,第二个项目、第三个项目测试过关的概率分别为x,y(x>y),且不同项目是否能够测试过关相互独立,记ξ为该生测试过关的项目数,其分布列如下表所示:
(1)求该生至少有2个项目测试过关的概率;
(2)求ξ的数学期望E(ξ).
| ξ | 0 | 1 | 2 | 3 |
| P | $\frac{6}{125}$ | a | b | $\frac{24}{125}$ |
(2)求ξ的数学期望E(ξ).
19.“y=sin(2x+φ)关于y轴对称”的( )条件是“$φ=\frac{π}{2}$”( )
| A. | 充分不必要 | B. | 必要不充分 | ||
| C. | 充要 | D. | 既不充分也不必要 |
3.已知双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右焦点分别为F1,F2,O为坐标原点,P是双曲线在第一象限上的点,直线PO,PF2分别交双曲线C左、右支于另一点M,N,|PF1|=2|PF2|,且∠MF2N=60°,则双曲线C的离心率为( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\sqrt{7}$ | D. | $\frac{2\sqrt{3}}{3}$ |
4.四棱锥A-BCDE,底面BCDE为梯形,EB∥DC,DC⊥平面ABC,AC=BC=EB=2DC,∠ACB=90°,AD与平面ABE所成角的正弦值为( )
| A. | $\frac{\sqrt{10}}{5}$ | B. | $\frac{\sqrt{5}}{5}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |