题目内容
已知f(α)=
.
(1)化简f(α);
(2)若α为第二象限角,sin(
+α)=
,求f(α).
sin(5π-α)cos(
| ||
| -tan(-19π-α)sin(-α) |
(1)化简f(α);
(2)若α为第二象限角,sin(
| π |
| 3 |
| 4 |
| 5 |
考点:运用诱导公式化简求值
专题:三角函数的求值
分析:(1)由条件利用诱导公式化简可得所给式子的值,可得结果.
(2)由条件利用同角三角函数的基本关系、两角和差的正弦公式求得f(α)的值.
(2)由条件利用同角三角函数的基本关系、两角和差的正弦公式求得f(α)的值.
解答:
解:(1)f(α)=
=
=
=sinα.
(2)∵sin(
+α)=
,
+α为第二或者第三象限角,可得cos(
+α)=-
,
∴f(α)=sinα=sin[(
+α)-
]=
×
-(-
)×
=
.
sin(5π-α)cos(
| ||
| -tan(-19π-α)sin(-α) |
sin(π-α)•cos(-
| ||
| -tan(-α)•(-sinα) |
| sinα•(-sinα)•tanα |
| -tanα•sinα |
(2)∵sin(
| π |
| 3 |
| 4 |
| 5 |
| π |
| 3 |
| π |
| 3 |
| 3 |
| 5 |
∴f(α)=sinα=sin[(
| π |
| 3 |
| π |
| 3 |
| 4 |
| 5 |
| 1 |
| 2 |
| 3 |
| 5 |
| ||
| 2 |
4+3
| ||
| 10 |
点评:本题主要考查应用诱导公式化简三角函数式,要特别注意符号的选取,这是解题的易错点;还考查了同角三角函数的基本关系、两角和差的正弦公式的应用,属于基础题.

练习册系列答案
相关题目
已知一直线的倾斜角为α,且满足45°≤α≤150°,则直线的斜率的取值范围为( )
A、[-
| ||||
B、(-∞,-
| ||||
C、(-∞,-
| ||||
D、[-
|
数列{an}的通项公式是an=(2n-5)(
)n,且an≤an0,则n0=( )
| 1 |
| 2 |
| A、2 | B、3 | C、4 | D、5 |
某台小型晚会由6个节目组成,演出顺序有如下要求:节目甲必须排在第四位、节目乙不能排在第一位,节目丙不能排在最后一位,该台晚会节目演出顺序的编排方案共有( )
| A、36种 | B、42种 |
| C、48种 | D、78种 |
sin(-240°)的值为( )
A、-
| ||||
B、
| ||||
C、-
| ||||
D、
|
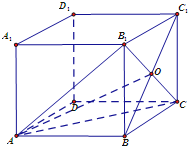 如图,在正方体ABCD-A1B1C1D1中,O是BC1与B1C的交点.
如图,在正方体ABCD-A1B1C1D1中,O是BC1与B1C的交点.