题目内容
求函数y=
(x∈R)的值域.
| x-2 |
| x2-2x+4 |
考点:函数的值域
专题:函数的性质及应用,不等式的解法及应用
分析:将函数解析式整理得到y=
,再利用基本不等式即可得到函数y=
(x∈R)的值域.
| x-2 |
| (x-2)2+2(x-2)+4 |
| x-2 |
| x2-2x+4 |
解答:
解:由于y=
=
,(x∈R),
则①当x=2时,y=0;
②当x≠2时,y=
=
(i)当x>2时,x-2>0,则(x-2)+
≥2
=4,则0<y≤
,
(ii)当x<2时,x-2<0,则(x-2)+
=-[(2-x)+
]≤-2
=-4,则-
≤y<0,
综上可知,函数y=
(x∈R)的值域为[-
,
].
| x-2 |
| x2-2x+4 |
| x-2 |
| (x-2)2+2(x-2)+4 |
则①当x=2时,y=0;
②当x≠2时,y=
| x-2 |
| (x-2)2+2(x-2)+4 |
| 1 | ||
(x-2)+
|
(i)当x>2时,x-2>0,则(x-2)+
| 4 |
| x-2 |
| 4 |
| 1 |
| 6 |
(ii)当x<2时,x-2<0,则(x-2)+
| 4 |
| x-2 |
| 4 |
| 2-x |
| 4 |
| 1 |
| 2 |
综上可知,函数y=
| x-2 |
| x2-2x+4 |
| 1 |
| 2 |
| 1 |
| 6 |
点评:考查函数值域的求法,解决本题时易忽视函数的有界性,要仔细区别,防止出错.

练习册系列答案
相关题目
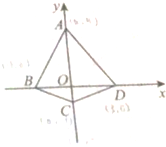 在平面直角坐标系xOy中,四边形ABCD的位置如图所示,A(0,4),B(-2,0),C(0,-1),D(3,0),动点P(x,y)在第一象限,且满足S△PAD=S△PBC,求点P的横、纵坐标满足的关系式(用x表示y),并写出x的取值范围.
在平面直角坐标系xOy中,四边形ABCD的位置如图所示,A(0,4),B(-2,0),C(0,-1),D(3,0),动点P(x,y)在第一象限,且满足S△PAD=S△PBC,求点P的横、纵坐标满足的关系式(用x表示y),并写出x的取值范围.