题目内容
集合A={x|x是奇数}，集合B={x∈R|x=4n±1，n∈Z}，则集合A，B之间的关系是 ．
考点：集合的包含关系判断及应用
专题：集合
分析：任取x∈A，可判断出x∈B，即A⊆B，任取x∈B，可判断出x∈A，即B⊆A，进而得到集合A，B之间的关系是．
解答：
解：任取x∈A，则x是奇数，
即x=2k+1，k∈Z，
当k为偶数，设k=2n，n∈Z，x=4n+1，n∈Z
当k为奇数时，设k=2n-1，n∈Z，x=4n-1，n∈Z
故A⊆B，
任取x∈B={x∈R|x=4n±1，n∈Z}，
∵x=4n（n∈Z）为偶数，
故x=4n±1，n∈Z为奇数，
故x∈A
∴B⊆A
∴A=B
故答案为：A=B
即x=2k+1，k∈Z，
当k为偶数，设k=2n，n∈Z，x=4n+1，n∈Z
当k为奇数时，设k=2n-1，n∈Z，x=4n-1，n∈Z
故A⊆B，
任取x∈B={x∈R|x=4n±1，n∈Z}，
∵x=4n（n∈Z）为偶数，
故x=4n±1，n∈Z为奇数，
故x∈A
∴B⊆A
∴A=B
故答案为：A=B
点评：本题考查的知识点是集合的包含关系判断及应用，熟练掌握集合关系的定义是解答的关键．
练习册系列答案
阅读快车系列答案
相关题目
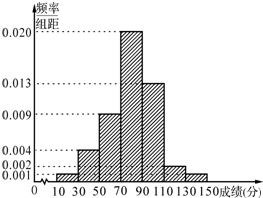某学校为了选拔学生参加“XX市中学生知识竞赛”，先在本校进行选拔测试（满分150分），若该校有100名学生参加选拔测试，并根据选拔测试成绩作出如图所示的频率分布直方图．