题目内容
双曲线
-
=1的一条渐近线的倾斜角为n，经过此双曲线的一个焦点且与其实轴垂直的直线与该双曲线相交于P，Q两点，则|PQ|的长度是多少？
| x2 |
| a2 |
| y2 |
| b2 |
考点：双曲线的简单性质
专题：计算题,圆锥曲线的定义、性质与方程
分析：由双曲线
-
=1的一条渐近线的倾斜角为n，可得tann=
，令x=c，则y=±
，从而可求|PQ|的长度．
| x2 |
| a2 |
| y2 |
| b2 |
| b |
| a |
| b2 |
| a |
解答：
解：∵双曲线
-
=1的一条渐近线的倾斜角为n，
∴tann=
，
令x=c，则
-
=1，∴y=±
，
∴|PQ|=
=2btann．
| x2 |
| a2 |
| y2 |
| b2 |
∴tann=
| b |
| a |
令x=c，则
| c2 |
| a2 |
| y2 |
| b2 |
| b2 |
| a |
∴|PQ|=
| 2b2 |
| a |
点评：本题考查双曲线的简单性质，考查学生的计算能力，属于基础题．
练习册系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
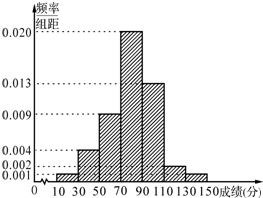某学校为了选拔学生参加“XX市中学生知识竞赛”，先在本校进行选拔测试（满分150分），若该校有100名学生参加选拔测试，并根据选拔测试成绩作出如图所示的频率分布直方图．