某车向正南方向开了S km后.向右转30°角.然后又开了2km.结果该车离出发点恰好2$\sqrt{3}$km.则S=($\sqrt{11}$-$\sqrt{3}$)km．题目和参考答案——青夏教育精英家教网—

题目内容

14．某车向正南方向开了S km后，向右转30°角，然后又开了2km，结果该车离出发点恰好2$\sqrt{3}$km，则S=（$\sqrt{11}$-$\sqrt{3}$）km．

分析作出图象，三点之间正好组成了一个知两边与一角的三角形，由余弦定理建立关于S的方程即可求得S的值．

解答解：由题意，如图所示，AB=Skm，BC=2km，AC=2$\sqrt{3}$km，∠ABC=150°．
由余弦定理可得12=S²+4-2×2×S×cos150°，
∴S²+2$\sqrt{3}$S-8=0，
∴S=$\sqrt{11}$-$\sqrt{3}$．
故答案为：（$\sqrt{11}$-$\sqrt{3}$）km．

点评本题考查解三角形的知识，其特点从应用题中抽象出三角形．根据数据特点选择合适的定理建立方程求解．属基础题．

练习册系列答案

5．等差数列{a_n}的公差为1，若S_n≥S₈对一切n∈N^*恒成立，则首项叫a₁的取值范围是（-8，-7）．

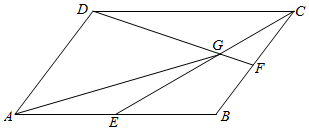
2．如图在平行四边形ABCD中，E、F分别是AB、BC边中点，线段CE、DF相交于点G，若$\overrightarrow{AB}$=$\overrightarrow{a}$，$\overrightarrow{AD}$=$\overrightarrow{b}$，则$\overrightarrow{AG}$=（　　）

A．

$\frac{4}{5}$$\overrightarrow{a}$+$\frac{3}{5}$$\overrightarrow{b}$

B．

$\frac{3}{5}$$\overrightarrow{a}$+$\frac{4}{5}$$\overrightarrow{b}$

C．

$\frac{5}{6}$$\overrightarrow{a}$+$\frac{2}{3}$$\overrightarrow{b}$

D．

$\frac{2}{3}$$\overrightarrow{a}$+$\frac{5}{6}$$\overrightarrow{b}$

9．已知点O为坐标原点，向量$\overrightarrow{OA}$=（1，2），$\overrightarrow{OB}$=（-2，1），若点C与点A关于直线y=x对称，则$\overrightarrow{CA}$$•\overrightarrow{BO}$=-3．

19．函数y=log_asine^x的导数是=$\frac{{e}^{x}cos{e}^{x}}{lna•sin{e}^{x}}$．

6．已知0＜α＜β，不等式ax²+bx+c＞0的解集为（α，β），求不等式（a+c-b）x²+（b-2a）x+a＞0的解集．

3．在平面直角坐标系xOy中，钝角α的终边与单位圆的交点为A且A点的纵坐标为$\frac{\sqrt{5}}{5}$，锐角β的终边与单位圆的交点为B且B点的横坐标为$\frac{2\sqrt{5}}{5}$．
（1）求sin（α+$\frac{π}{4}$）；
（2）求tan（2α+β）．

9．角α的终边上一点的坐标为$（2sin\frac{2π}{3}，2cos\frac{2π}{3}）$，则sinα等于（　　）

$-\frac{{\sqrt{3}}}{2}$

D．

$\frac{1}{2}$

试题分类