题目内容
2.如图在平行四边形ABCD中,E、F分别是AB、BC边中点,线段CE、DF相交于点G,若$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$,则$\overrightarrow{AG}$=( )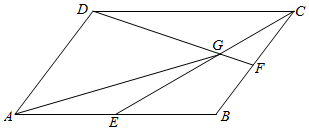
| A. | $\frac{4}{5}$$\overrightarrow{a}$+$\frac{3}{5}$$\overrightarrow{b}$ | B. | $\frac{3}{5}$$\overrightarrow{a}$+$\frac{4}{5}$$\overrightarrow{b}$ | C. | $\frac{5}{6}$$\overrightarrow{a}$+$\frac{2}{3}$$\overrightarrow{b}$ | D. | $\frac{2}{3}$$\overrightarrow{a}$+$\frac{5}{6}$$\overrightarrow{b}$ |
分析 利用向量共线定理可得:$\overrightarrow{AG}$=x$\overrightarrow{AE}$+(1-x)$\overrightarrow{AC}$,$\overrightarrow{AG}$=y$\overrightarrow{AF}$+(1-y)$\overrightarrow{AD}$,又$\overrightarrow{AE}$=$\frac{1}{2}\overrightarrow{AB}$=$\frac{1}{2}$$\overrightarrow{a}$,$\overrightarrow{AF}$=$\overrightarrow{AB}$+$\overrightarrow{BF}$=$\overrightarrow{a}+\frac{1}{2}\overrightarrow{b}$,$\overrightarrow{AC}$=$\overrightarrow{AB}$+$\overrightarrow{AD}$=$\overrightarrow{a}+\overrightarrow{b}$.代入化简即可得出.
解答 解:利用向量共线定理可得:$\overrightarrow{AG}$=x$\overrightarrow{AE}$+(1-x)$\overrightarrow{AC}$,$\overrightarrow{AG}$=y$\overrightarrow{AF}$+(1-y)$\overrightarrow{AD}$,
$\overrightarrow{AE}$=$\frac{1}{2}\overrightarrow{AB}$=$\frac{1}{2}$$\overrightarrow{a}$,$\overrightarrow{AF}$=$\overrightarrow{AB}$+$\overrightarrow{BF}$=$\overrightarrow{a}+\frac{1}{2}\overrightarrow{b}$,$\overrightarrow{AC}$=$\overrightarrow{AB}$+$\overrightarrow{AD}$=$\overrightarrow{a}+\overrightarrow{b}$.
∴x•$\frac{1}{2}\overrightarrow{a}$+(1-x)•$(\overrightarrow{a}+\overrightarrow{b})$=$y•(\overrightarrow{a}+\frac{1}{2}\overrightarrow{b})$+(1-y)$•\overrightarrow{b}$,
整理为:(2-x-2y)$\overrightarrow{a}$+(y-2x)$\overrightarrow{b}$=$\overrightarrow{0}$,
∴$\left\{\begin{array}{l}{2-x-2y=0}\\{y-2x=0}\end{array}\right.$,解得x=$\frac{2}{5}$,y=$\frac{4}{5}$.
∴$\overrightarrow{AG}$=$\frac{4}{5}\overrightarrow{a}$+$\frac{3}{5}\overrightarrow{b}$.
故选:A.
点评 本题考查了向量的三角形法则、平行四边形法则、向量共线定理、向量共面定理,考查了推理能力与计算能力,属于中档题.

 走进文言文系列答案
走进文言文系列答案| A. | 2$\sqrt{3}$ | B. | $\sqrt{3}$ | C. | 4$\sqrt{2}$ | D. | 2$\sqrt{2}$ |
| A. | y=±2x | B. | y=±$\frac{1}{2}$x | C. | y=$±\sqrt{5}$x | D. | y=$±\frac{\sqrt{5}}{2}$x |
 如图,已知菱形ABCD中,点P为线段CD上一点,且$\overrightarrow{CP}$=$λ\overrightarrow{CD}$(0≤λ≤1).
如图,已知菱形ABCD中,点P为线段CD上一点,且$\overrightarrow{CP}$=$λ\overrightarrow{CD}$(0≤λ≤1).