题目内容
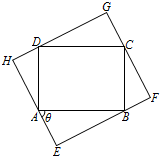 如图所示,某住宅小区有一个矩形休闲广场ABCD,其中AB=40 米,BC=30 米,根据小区业主建议,需将其扩大成矩形区域EFGH,要求A、B、C、D四个点分别在矩形EFGH的四条边(不含顶点)上.设∠BAE=θ,EF长为y米.
如图所示,某住宅小区有一个矩形休闲广场ABCD,其中AB=40 米,BC=30 米,根据小区业主建议,需将其扩大成矩形区域EFGH,要求A、B、C、D四个点分别在矩形EFGH的四条边(不含顶点)上.设∠BAE=θ,EF长为y米.(1)将y表示成θ的函数;
(2)求矩形区域EFGH的面积的最大值.
考点:三角函数的最值,函数解析式的求解及常用方法,三角函数中的恒等变换应用
专题:三角函数的求值
分析:(1)由几何图形结合解直角三角形知识将y表示成θ的函数;
(2)直接由矩形面积等于长乘宽列出面积关于θ的表达式,结合三角函数的化简与求值得答案.
(2)直接由矩形面积等于长乘宽列出面积关于θ的表达式,结合三角函数的化简与求值得答案.
解答:
解:(1)如图,
 由∠BAE=θ,∠E=90°,得∠ABE=90°-θ,
由∠BAE=θ,∠E=90°,得∠ABE=90°-θ,
再由∠ABC=90°,得∠CBF=θ,同理∠DCG=θ.
由AB=40(米),BC=30(米),四边形ABCD为矩形,得DC=40(米),
因此,EF=EB+BF=40sinθ+30cosθ(米),
因此y=40sinθ+30cosθ(0°<θ<90°);
(2)SEFGH=EF•FG=1200sin2θ+1200cos2θ+2500sinθcosθ
=1200+1250sin2θ,(0°<θ<90°).
因此θ=45°时,SEFGH取到最大值,最大值为2450.
因此,矩形区域EFGH的面积的最大值为2450平方米.
 由∠BAE=θ,∠E=90°,得∠ABE=90°-θ,
由∠BAE=θ,∠E=90°,得∠ABE=90°-θ,再由∠ABC=90°,得∠CBF=θ,同理∠DCG=θ.
由AB=40(米),BC=30(米),四边形ABCD为矩形,得DC=40(米),
因此,EF=EB+BF=40sinθ+30cosθ(米),
因此y=40sinθ+30cosθ(0°<θ<90°);
(2)SEFGH=EF•FG=1200sin2θ+1200cos2θ+2500sinθcosθ
=1200+1250sin2θ,(0°<θ<90°).
因此θ=45°时,SEFGH取到最大值,最大值为2450.
因此,矩形区域EFGH的面积的最大值为2450平方米.
点评:本题考查了简单的数学建模思想方法,考查了三角函数的化简与求值,正确将y表示成θ的函数是解答该题的关键,是中档题.

练习册系列答案
相关题目
函数f(x)=x2-2x零点个数为( )
| A、1 | B、2 | C、3 | D、4 |

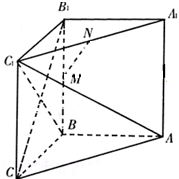 如图所示,在直角三棱柱A1B1C1-ABC中,∠ABC=90°,M、N分别为B1B、A1C1的中点.
如图所示,在直角三棱柱A1B1C1-ABC中,∠ABC=90°,M、N分别为B1B、A1C1的中点.