题目内容
已知函数y=f（x）的图象如图所示，则函数y=f′（x）的图象可能是 （填序号）
考点：利用导数研究函数的单调性
专题：计算题,函数的性质及应用,导数的综合应用
分析：观察函数y=f（x）的图象知，f（x）在（-∞，0]上是增函数，在[0，+∞）上是减函数；从而确定导数的正负，从而求解．
解答：
解：观察函数y=f（x）的图象知，
f（x）在（-∞，0]上是增函数，在[0，+∞）上是减函数；
故当x∈（-∞，0]时，f′（x）＞0，
当x∈[0，+∞）时，f′（x）＜0；
故结合四个图象知，第②个可能；
故答案为：②．
f（x）在（-∞，0]上是增函数，在[0，+∞）上是减函数；
故当x∈（-∞，0]时，f′（x）＞0，
当x∈[0，+∞）时，f′（x）＜0；
故结合四个图象知，第②个可能；
故答案为：②．
点评：本题考查了导数的综合应用，同时考查了数形结合的思想应用，属于基础题．
练习册系列答案
相关题目
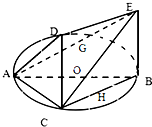如图，一简单几何体ABCDE的一个面ABC内接于圆O，G、H分别是AE、BC的中点，AB是圆O的直径，四边形DCBE为平行四边形，且DC⊥平面ABC．
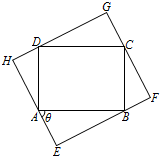如图所示，某住宅小区有一个矩形休闲广场ABCD，其中AB=40 米，BC=30 米，根据小区业主建议，需将其扩大成矩形区域EFGH，要求A、B、C、D四个点分别在矩形EFGH的四条边（不含顶点）上．设∠BAE=θ，EF长为y米．