题目内容
过点P（3，5）且与圆（x-2）2+（y-3）2=1相切的切线方程是 ．
考点：圆的切线方程
专题：直线与圆
分析：根据直线和圆相切的位置关系即可得到结论．
解答：
解：圆心坐标为（2，3），半径r=1，
若切线斜率k不存在，
则x=3，圆心到直线的距离d=3-2=1，满足条件．
若切线斜率k存在，则切线方程为y-5=k（x-3），
即kx-y+5-3k=0，
则圆心到直线的距离d=
=
=1，
解得k=
，
即圆的切线方程为3x-4y+11=0和x=3，
故答案为：3x-4y+11=0和x=3
若切线斜率k不存在，
则x=3，圆心到直线的距离d=3-2=1，满足条件．
若切线斜率k存在，则切线方程为y-5=k（x-3），
即kx-y+5-3k=0，
则圆心到直线的距离d=
| |2k-3+5-3k| | ||
|
| |2-k| | ||
|
解得k=
| 3 |
| 4 |
即圆的切线方程为3x-4y+11=0和x=3，
故答案为：3x-4y+11=0和x=3
点评：本题主要考查直线方程的求解，利用直线和圆相切转化为圆心到直线的距离d=R是解决本题的关键．
练习册系列答案
相关题目
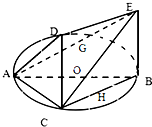如图，一简单几何体ABCDE的一个面ABC内接于圆O，G、H分别是AE、BC的中点，AB是圆O的直径，四边形DCBE为平行四边形，且DC⊥平面ABC．若函数f（x）为偶函数，x＞0时，f（x）单调递增，P=f（-π），Q=f（e），R=f（
），则P，Q，R的大小为（ ）
| 2 |
| A、R＞Q＞P |
| B、Q＞R＞P |
| C、P＞R＞Q |
| D、P＞Q＞R |
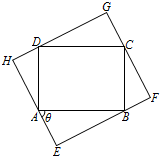如图所示，某住宅小区有一个矩形休闲广场ABCD，其中AB=40 米，BC=30 米，根据小区业主建议，需将其扩大成矩形区域EFGH，要求A、B、C、D四个点分别在矩形EFGH的四条边（不含顶点）上．设∠BAE=θ，EF长为y米．
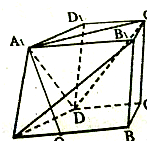如图，在四棱柱ABCD-A1B1C1D1中，底面ABCD是一个直角梯形，AB∥CD，∠ABC=90°．CD=3，BC=2，AB=5，AA1=2已知曲线x2+y+1=0与双曲线x2-
=1（b＞0）的渐近线相切，则此双曲线的焦距等于（ ）
| y2 |
| b2 |
A、2
| ||
B、2
| ||
| C、4 | ||
D、2
|