题目内容
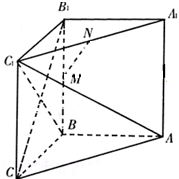 如图所示,在直角三棱柱A1B1C1-ABC中,∠ABC=90°,M、N分别为B1B、A1C1的中点.
如图所示,在直角三棱柱A1B1C1-ABC中,∠ABC=90°,M、N分别为B1B、A1C1的中点.(1)求证:平面ABC1⊥平面B1BC;
(2)求证:MN∥平面ABC1.
考点:直线与平面平行的判定,平面与平面垂直的判定
专题:空间位置关系与距离
分析:(I)根据直三棱柱的性质,利用面面垂直性质定理证出AB⊥平面BB1C1,得出AB⊥CB1.正方形BCC1B1中,对角线CB1⊥BC1,由线面垂直的判定定理可证出CB1⊥平面ABC1;
(II)取AC1的中点F,连BF、NF,利用三角形中位线定理和平行四边形的性质,证出EF∥BM且EF=BM,从而得到BMNF是平行四边形,可得MN∥BF,结合线面平行判定定理即可证出MN∥面ABC1.
(II)取AC1的中点F,连BF、NF,利用三角形中位线定理和平行四边形的性质,证出EF∥BM且EF=BM,从而得到BMNF是平行四边形,可得MN∥BF,结合线面平行判定定理即可证出MN∥面ABC1.
解答:
解:(Ⅰ)在直三棱柱ABC-A1B1C1中,
侧面BB1C1C⊥底面ABC,且侧面BB1C1C∩底面ABC=BC,
∵∠ABC=90°,即AB⊥BC,
∴AB⊥平面BB1C1 …(2分
∵CB1?平面BB1C1C,∴AB⊥CB1.…(4分)
∵BC=CC1,CC1⊥BC,∴BCC1B1是正方形,
∴CB1⊥BC1,
∵AB∩BC1=B,∴CB1⊥平面ABC1,
CB1?平面B1BC;
∴平面ABC1⊥平面B1BC;
(Ⅱ)取AC1的中点F,连BF、NF.…(7分)如图
在△AA1C1中,N、F是中点,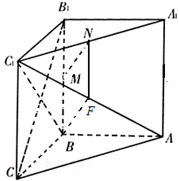
∴NF∥AA1,NF=
AA1
又∵正方形BCC1B1中,BM∥AA1,BM=
AA1
∴NF∥BM,且NF=BM…(8分)
故四边形BMNF是平行四边形,可得MN∥BF,…(10分)
∵BF?面ABC1,MN?平面ABC1,
∴MN∥面ABC1…(12分)
侧面BB1C1C⊥底面ABC,且侧面BB1C1C∩底面ABC=BC,
∵∠ABC=90°,即AB⊥BC,
∴AB⊥平面BB1C1 …(2分
∵CB1?平面BB1C1C,∴AB⊥CB1.…(4分)
∵BC=CC1,CC1⊥BC,∴BCC1B1是正方形,
∴CB1⊥BC1,
∵AB∩BC1=B,∴CB1⊥平面ABC1,
CB1?平面B1BC;
∴平面ABC1⊥平面B1BC;
(Ⅱ)取AC1的中点F,连BF、NF.…(7分)如图
在△AA1C1中,N、F是中点,

∴NF∥AA1,NF=
| 1 |
| 2 |
又∵正方形BCC1B1中,BM∥AA1,BM=
| 1 |
| 2 |
∴NF∥BM,且NF=BM…(8分)
故四边形BMNF是平行四边形,可得MN∥BF,…(10分)
∵BF?面ABC1,MN?平面ABC1,
∴MN∥面ABC1…(12分)
点评:本题给出底面为直角三角形的直三棱柱,在已知侧棱与底面直角边长相等的情况下证明线面垂直.着重考查了空间直线与平面平行、垂直的判定与性质等知识,属于中档题.

练习册系列答案
 每课必练系列答案
每课必练系列答案
相关题目
在区间[-5,5]内随机取出一个实数a,则a∈(0,1)的概率为( )
| A、0.5 | B、0.3 |
| C、0.2 | D、0.1 |
某人午觉醒来,发现表停了,他打开收音机,想听电台报时,则他等待的时间不超过10分钟的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
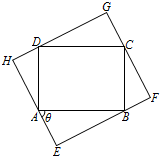 如图所示,某住宅小区有一个矩形休闲广场ABCD,其中AB=40 米,BC=30 米,根据小区业主建议,需将其扩大成矩形区域EFGH,要求A、B、C、D四个点分别在矩形EFGH的四条边(不含顶点)上.设∠BAE=θ,EF长为y米.
如图所示,某住宅小区有一个矩形休闲广场ABCD,其中AB=40 米,BC=30 米,根据小区业主建议,需将其扩大成矩形区域EFGH,要求A、B、C、D四个点分别在矩形EFGH的四条边(不含顶点)上.设∠BAE=θ,EF长为y米.