题目内容
已知抛物线的顶点坐标为原点，对称轴为x轴，且与圆x2+y2=16相交的公共弦长等于4
，则这个抛物线的方程为 ．
| 3 |
考点：抛物线的简单性质
专题：计算题,圆锥曲线的定义、性质与方程
分析：设出抛物线方程，利用抛物线与圆x2+y2=16相交的公共弦长等于4
，确定弦的端点的坐标，代入抛物线方程，可得结论．
| 3 |
解答：
解：由题意，开口向右时，设抛物线方程为y2=2px（p＞0）
∵抛物线与圆x2+y2=16相交的公共弦长等于4
，
∴弦的端点的坐标为（2，±2
）
代入抛物线方程可得4p=12，∴p=3，∴抛物线方程为y2=6x；
同理可得开口向左时，抛物线方程为y2=-6x．
故答案为：y2=6x或y2=-6x．
∵抛物线与圆x2+y2=16相交的公共弦长等于4
| 3 |
∴弦的端点的坐标为（2，±2
| 3 |
代入抛物线方程可得4p=12，∴p=3，∴抛物线方程为y2=6x；
同理可得开口向左时，抛物线方程为y2=-6x．
故答案为：y2=6x或y2=-6x．
点评：本题考查抛物线方程，考查学生的计算能力，属于基础题．
练习册系列答案
相关题目
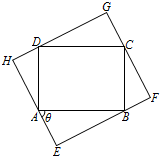如图所示，某住宅小区有一个矩形休闲广场ABCD，其中AB=40 米，BC=30 米，根据小区业主建议，需将其扩大成矩形区域EFGH，要求A、B、C、D四个点分别在矩形EFGH的四条边（不含顶点）上．设∠BAE=θ，EF长为y米．