题目内容
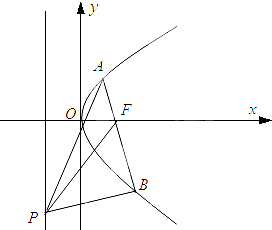 已知抛物线y2=2px(p>0)上点M(3,m)到焦点F的距离为4.
已知抛物线y2=2px(p>0)上点M(3,m)到焦点F的距离为4.(Ⅰ)求抛物线方程;
(Ⅱ)点P为准线上任意一点,AB为抛物线上过焦点的任意一条弦,设直线PA,PB,PF的斜率为k1,k2,k3,问是否存在实数λ,使得k1+k2=λk3恒成立.若存在,请求出λ的值;若不存在,请说明理由.
考点:直线与圆锥曲线的关系
专题:存在型,圆锥曲线的定义、性质与方程
分析:(Ⅰ)由抛物线的定义:到焦点的距离等于到准线的距离,即可求出p,从而得到方程;
(Ⅱ)求出焦点和准线,设出直线AB,联立方程,消去x得到y的方程,运用韦达定理,设A(x1,y1),B(x2,y2),P(-1,t),运用斜率公式,化简整理,注意点在抛物线上,且全部转化为y的式子,即可判断.
(Ⅱ)求出焦点和准线,设出直线AB,联立方程,消去x得到y的方程,运用韦达定理,设A(x1,y1),B(x2,y2),P(-1,t),运用斜率公式,化简整理,注意点在抛物线上,且全部转化为y的式子,即可判断.
解答:
解:(I)抛物线y2=2px(p>0)的焦点为(
,0),准线为x=-
,
由抛物线的定义可知:4=3+
,p=2
∴抛物线方程为y2=4x;
(II)由于抛物线y2=4x的焦点F为(1,0),准线为x=-1,
设直线AB:x=my+1,与y2=4x联立,消去x,整理得:
y2-4my-4=0,
设A(x1,y1),B(x2,y2),P(-1,t),有
易知k3=-
,而k1+k2=
+
=
=
=
=-t=2k3
∴存在实数λ=2,使得k1+k2=λk3恒成立.
| p |
| 2 |
| p |
| 2 |
由抛物线的定义可知:4=3+
| p |
| 2 |
∴抛物线方程为y2=4x;
(II)由于抛物线y2=4x的焦点F为(1,0),准线为x=-1,
设直线AB:x=my+1,与y2=4x联立,消去x,整理得:
y2-4my-4=0,
设A(x1,y1),B(x2,y2),P(-1,t),有
|
易知k3=-
| t |
| 2 |
| y1-t |
| x1+1 |
| y2-t |
| x2+1 |
=
| (x2+1)(y1-t)+(x1+1)(y2-t) |
| (x1+1)(x2+1) |
(
| ||||||||
(
|
=
| -t(4m2+4) |
| 4m2+4 |
∴存在实数λ=2,使得k1+k2=λk3恒成立.
点评:本题主要考查直线与抛物线的位置关系,考查抛物线的定义、性质和方程,同时考查联立方程,运用韦达定理,运用斜率公式,考查运算化简能力,是一道中档题.

练习册系列答案
相关题目
已知圆柱的底面半径为2,高为3,用一个与底面不平行的平面去截,若所截得的截面为椭圆,则椭圆的离心率的最大值为( )
| A、1 | ||
B、
| ||
C、
| ||
D、
|
如果命题“¬(p∧q)”为假命题,则( )
| A、p、q均为真命题 |
| B、p、q均为假命题 |
| C、p、q至少有一个为真命题 |
| D、p、q至多有一个为真命题 |
已知一个60°的二面角的棱上有两点A,B,AC,BD分别是在这个二面角的两个面内垂直于AB的线段,若AB=4,AC=6,BD=8,则CD=( )
A、2
| ||
B、2
| ||
C、2
| ||
| D、10 |
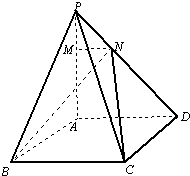 已知四棱锥P-ABCD中,底面ABCD为菱形,PA⊥底面ABCD,∠BAD=120°,PA=AB=2
已知四棱锥P-ABCD中,底面ABCD为菱形,PA⊥底面ABCD,∠BAD=120°,PA=AB=2
 在棱长为2的正方体ABCD-A1B1C1D1中,O为正方形A1B1C1D1的中心,点P在棱CC1上,且CC1=2PC.
在棱长为2的正方体ABCD-A1B1C1D1中,O为正方形A1B1C1D1的中心,点P在棱CC1上,且CC1=2PC.