题目内容
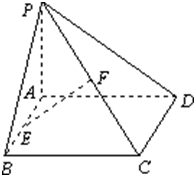 已知矩形ABCD所在平面外一点P,PA⊥平面ABCD,E、F分别是AB、PC的中点,且PA=AD.
已知矩形ABCD所在平面外一点P,PA⊥平面ABCD,E、F分别是AB、PC的中点,且PA=AD.(1)求证:EF∥平面PAD;
(2)求证:面PEC⊥面PCD.
考点:平面与平面垂直的判定,直线与平面平行的判定
专题:空间位置关系与距离
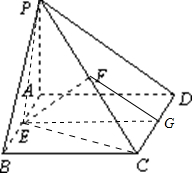
分析:(1)作CD的中点G,连结FG,EG,先证明出FG∥PD,EG∥AD,根据面面平行的判定定理证明出平面EFG∥平面ADP,进而根据面面平行的性质证明出EF∥平面ADP.
(2)根据线面垂直的判定定理证明出CD⊥EFG,则EF⊥CD可证,进而证明出△PEA≌△CEB得知PE=CE,证明出EF⊥PC,最后利用线面垂直的判定定理证明出EF⊥平面PCD.
最后利用面面垂直的判定定理证明出面PEC⊥面PCD.
(2)根据线面垂直的判定定理证明出CD⊥EFG,则EF⊥CD可证,进而证明出△PEA≌△CEB得知PE=CE,证明出EF⊥PC,最后利用线面垂直的判定定理证明出EF⊥平面PCD.
最后利用面面垂直的判定定理证明出面PEC⊥面PCD.
解答:
(1)作CD的中点G,连结FG,EG,
∵E,F,G均为中点,
∴FG∥PD,EG∥AD,
∵FG?平面ADP,EG?平面ADP,
∴FG∥平面ADP,EG∥平面ADP,
∵FG∩EG=G,FG?平面EFG,EG?平面EFG,
∴平面EFG∥平面ADP,
∵EF?平面EFG,
∴EF∥平面ADP.
(2)∵PA⊥平面ABCD,CD?平面ABCD,
∴PA⊥CD,
∵CD⊥AD,PA∩AD=A,PA?平面ADP,AD?平面ADP,
∴CD⊥平面ADP,
∵平面EFG∥平面ADP,
∴CD⊥平面EFG,
∵EF?平面EFG,
∴CD⊥EF,
∵PA=AD=BC,∠A=∠B,BE=AE,
∴△PEA≌△CEB,
∴PE=EC,
∵F为PC的中点,
∴EF⊥PC,
∵PC?平面PCD,CD?平面PCD,PC∩CD=C,
∴EF⊥平面PCD.
∵EF?面PEC,
∴面PEC⊥面PCD.
∵E,F,G均为中点,
∴FG∥PD,EG∥AD,
∵FG?平面ADP,EG?平面ADP,
∴FG∥平面ADP,EG∥平面ADP,
∵FG∩EG=G,FG?平面EFG,EG?平面EFG,
∴平面EFG∥平面ADP,
∵EF?平面EFG,
∴EF∥平面ADP.
(2)∵PA⊥平面ABCD,CD?平面ABCD,
∴PA⊥CD,
∵CD⊥AD,PA∩AD=A,PA?平面ADP,AD?平面ADP,
∴CD⊥平面ADP,
∵平面EFG∥平面ADP,
∴CD⊥平面EFG,
∵EF?平面EFG,
∴CD⊥EF,
∵PA=AD=BC,∠A=∠B,BE=AE,
∴△PEA≌△CEB,
∴PE=EC,
∵F为PC的中点,
∴EF⊥PC,
∵PC?平面PCD,CD?平面PCD,PC∩CD=C,
∴EF⊥平面PCD.
∵EF?面PEC,
∴面PEC⊥面PCD.

点评:本题主要考查了线面垂直和面面垂直的判定定理的应用.证明面面垂直的主要方法一般是先证明出线面垂直,进而判断出面面垂直.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
已知一个60°的二面角的棱上有两点A,B,AC,BD分别是在这个二面角的两个面内垂直于AB的线段,若AB=4,AC=6,BD=8,则CD=( )
A、2
| ||
B、2
| ||
C、2
| ||
| D、10 |
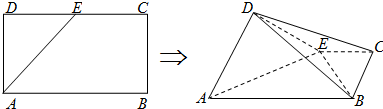
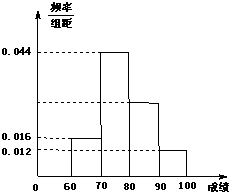 某校50名学生在一次科普知识竞赛中,初赛成绩全部介于60与100之间,将初赛成绩按如下方式分成四组:第一组[60,70],第二组[70,80],…,第四组[90,100].如图是按上述分组方法得到的频率分布直方图.
某校50名学生在一次科普知识竞赛中,初赛成绩全部介于60与100之间,将初赛成绩按如下方式分成四组:第一组[60,70],第二组[70,80],…,第四组[90,100].如图是按上述分组方法得到的频率分布直方图. 在棱长为2的正方体ABCD-A1B1C1D1中,O为正方形A1B1C1D1的中心,点P在棱CC1上,且CC1=2PC.
在棱长为2的正方体ABCD-A1B1C1D1中,O为正方形A1B1C1D1的中心,点P在棱CC1上,且CC1=2PC.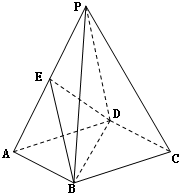 如图,在四棱柱P-ABCD中,底面ABCD是矩形,E是棱PA的中点,PD⊥BC.求证:
如图,在四棱柱P-ABCD中,底面ABCD是矩形,E是棱PA的中点,PD⊥BC.求证: