题目内容
18．已知x2≤1，且a-2≥0，求函数f（x）=x2+ax+3的最值．分析 求出f（x）的对称轴，判断区间[-1，1]在对称轴的右边，且为增区间，即可得到最值．
解答 解：由x2≤1，且a-2≥0，可得
-1≤x≤1，a≥2，
函数f（x）=x2+ax+3的对称轴为x=-$\frac{a}{2}$，
且-$\frac{a}{2}$≤-1，
即有区间[-1，1]为增区间，
可得f（x）的最小值为f（-1）=4-a；
最大值为f（1）=4+a．
点评 本题考查二次函数的最值的求法，注意对称轴和区间的关系，考查运算能力，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
8．已知函数y=x（x-2）的定义域为[a，b]，值域为[-1，3]，则点（a，b）对应图中的（ ）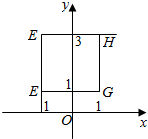
| A． | 点H（1，3）和点F（-1，1） | B． | 线段EF和线段GH | C． | 线段EH和线段FG | D． | 线段EF和线段EH |
6．过圆x2+y2=4上一点（$\sqrt{2}$，1）的切线方程为（ ）
| A． | x+$\sqrt{2}$y=4 | B． | $\sqrt{2}$x+y=3 | C． | $\sqrt{2}$x+y=4 | D． | x+$\sqrt{2}$y=2 |